Shape functions

Introduction

Fivefold symmetry

The progress of solar activity reminds in some aspects the hands and fingers ...
Theodor Landscheidt introduced the following designation:

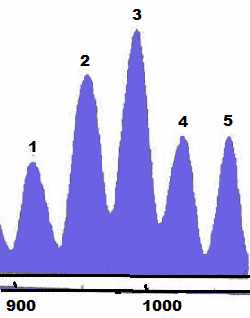
• Big hand 180 years (on the picture)
• Big finger 36 years
• Small finger 7-8 years

It is a two-layer five-symmetry, see Landscheidt's designations.

Sixfold symmetry

Model of shifted cycles (originated c. in 2000) came from inspiration by the Landscheidt's suggestion, from the Babylonian cycle and from observations of Jupiter-Saturn conjunctions. see Shift of cycles.

Here, the symmetry is six-fold with a 35-year finger and 210-year hand..

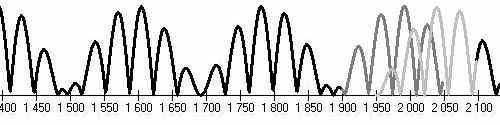
Cycles in the individual approx. 850-900 years stages are formed by composition of two components with periods P = 3∙(J, S) = 59.58 years and Q = (U, N) /2=85.72 years. The phase shift of the 60-year cycle changes in the each stage (according to detachments of the Jupiter-Saturn conjunctions).

Pavel Kalenda modified this model by modulating with a 1000-year period to form:

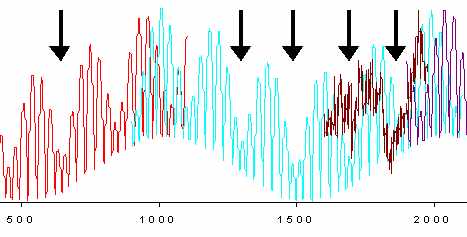
Composition of functions

Hypothesis of planet X

The 850 year cycle (cycle of two Babylonian periods) can be imagined as a combination of two cycles: 107 years and 285 years (in ratio 3:8). Assuming the existence of the planet X with a period of approximately 390 years, the periods of the cycles correspond to the synodic periods of Uranus and Neptune with respect to X: (U, X) = 107 years, (N, X) = 285 years. Multiples of both of these periods were observed in analyzes of climatic changes.

These cycles were supplemented by a cycle of conjunctions Uranus-Neptune (with a period of about 171 years), whose potential influence on the climate has already been considered earlier (the cycle is close to the frequently cited 178-year cycle).

It was then to guess phases of the cycle, ie the potential position of planet X. The following function was derived from the comparison of resonance courses and the known courses of solar activity :
cos(2π*(x-2027)/286.8)+cos(2π*(x-2005)/107.3)+cos(2π *(x-1907)/171.4).
The chart of this function is:

For a more detailed description see Planet X.

Vukcevic's shapes

Milivoj.A.Vukcevic introduced (at work in y.2004) cycles with periods (J, S) = 19.859 years and 2J = 23.724 years.

The beats of these periods are approximately ((J, S), 2J) = 122 years, for the last century, Vukcevic has given a period of 118 years.
In addition to this period, Vukcevic works with a period of about 288 years (287-290 years).

The core of this theory - judging according to the periods of cycles (122 years, 288 years) - is close to the core of the above-mentioned model of Planet X. But there is one difference and it turns out to be substantial: the 122-year period is significantly longer than the previously considered period (U, X) = 107 years. (A few consecutive cycles make a difference of tens of years ...)

Here is a little more detail on Vukcevic's theory: Influence of planets on solar activity.

Functions according to Zharkova

Valentina Zharková derived two basic components of the sun magnetic field. These components resemble Vukcevic's functions.

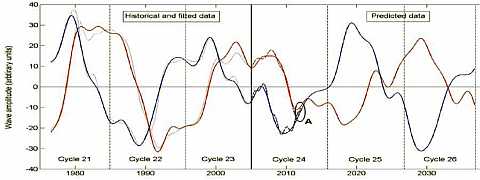
The following curves are based on a model inspired by Vukcevic's functions. The first of these features is the distances of Jupiter-Saturn, the second of Jupiter's actions. Functions are generated from real planetary motion provided some reversal of Jupiter's reversal (polarity reversal of magnetic fields ...)

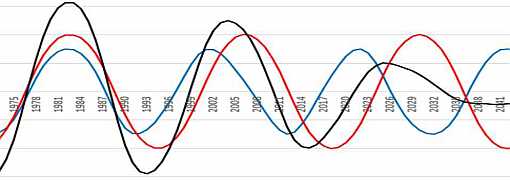
We will look at the model in the next paragraph.

Reverse polarity of Jupiter?

The mystery in Vukcevic's theory is the period of 2J, ie twice the orbital period of Jupiter. The first possible explanation was that Jupiter action somehow combine with polarity on the sun. E.g. different action of Jupiter in 1993 and in 2005 (in both cases it was Jupiter aphelion) could be explained by the fact that around 2000 the Sun reversed!? The effect of Jupiter (+ or -) would then differ by the number of the solar cycle (even / odd), which could eventually clarify the rule of lower and higher cycles (Gnevysev-Ohl).

But this system does not lead to a goal. To achieve Vukcevic's functions from real motion of planets, not the Sun have to be reversed, but the planet Jupiter (in each passing through perihelion) ...

In addition to matching the Zharková curves, the Maunder minimum results from this model:

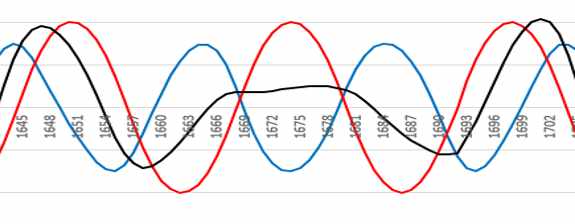
And also Dalton's minimum:

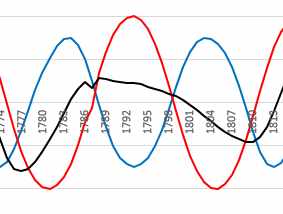
Curve amplitudes follow an approximately 120-year period that matches well a real shape of the activity. The worst predictions give the graphs at a time when both basic curves (blue and red) proceed in parallel (see eg 1725-1750, 1850-1875, 1975-2000 ..) ?!

Jupiter and extremes of activity

In Maunder's minimum (around 1626-1685) and Dalton's minimum (1805-1830) longer cycles corresponding to the Jupiter period are observed. Jupiter's aphelion seems to determine activity peaks, "Jupiter is waving with barycentre" (Pavel Kalenda), barycentre is deflected by conjunction of planets Uranus-Neptune.

But in 1990, there was also a conjunction of Uranus-Neptune, but Jupiter does not wave with barycentre!? Times of the Jupiter aphelion seem to be synchronous for the last with extremes of years 1947, 1958 and at most 1969.

This suggests that the barycentrum of 1990 was balanced by some planet X (somewhere near the line Uranus-Neptune ..!??)

Covering the climatic periods

In the following considerations we come out of the extremes in the years around 1372 and 1958, between which somewhere in the middle (1665) Maunder minimum is observed. We choose 2 functions with periods (very close to Vukcevic's periods) 287 years and 115 years. These periods have ratio 5:2, the common divisor is about 57.5 years, the common multiple is approximately 575 years.

The curve follows: 30*cos(6.28*(x - 1964)/287) + 30*cos(6.28*(x - 1964)/115)

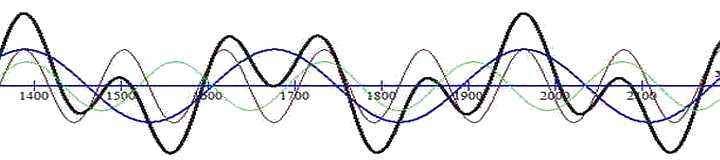
If the graph matches reality, then it would be "of a similar nature":

• maxima of the y.816, 1372, 1958
• Oort's and Maunder's minimum and year 536 (called Horibilis)
• Periods (1200,Wolf's 1300) and (Dalton 1810,1900)
• Sporer's and Dalton's (just reverse in time)

Considering that (U, N) = 171 years = 3 * 57 years, also conjunctions (U, N) fit into these cycles (with certain accuracy). The course of conjunctions is also projected into the graph (a weak green curve, -20 * cos (6.28 * (x - 1820) / 171)) but it is not included to the total.

According to Theodor Landscheidt, the 180-year cycles 1630-1810 and 1810-1990 are in antiphase. A similar course can be observed here in the graph.

Period of 230 years

Every 2 periods of 115 years give rise to "small pluvials" that were described by Zdeněk Vašků. Their mean period from the author's specified data results to ben 2 * 115 = 230 years.
The centers of the periods are around I.1100, II.1330, III.1560, IV.1790, V.2020. (Pluto does not fit into this raster because it is in perihels with a 250-year period ...)

Period of 860-870 years

Three periods of 287-289 years give approximately 865 years. This is close to the observed Laplace Jupiter-Saturn period (884 years?)

Among the famous large eruptions of year 79 (Vesuvius) and year 1815 (Tambora) lie in the middle year 947. The Paektu (Pektu-San, Korea) volcano erupted in the period of about 945-948. The distances of these three events are 868 years, ie about 3 * 289 years.

Hallstatt symmetry

Similar curves appear in the graph about every 2 * 287 years i.e. every about 575 years. This period corresponds to a quarter of the Hallstatt cycle of 2300 years, which Wilson already pointed out.

Some symmetry axes appear in the conjunctions of Venus-Earth-Jupiter, for the years 111.5, 687.1, 1262.6 and 1838.2. These points form minima on the curve cos(6.28 * (x - 1982.1) /287.78), resp. it is every second minimum. (The graph above shows the curve cos(6.28 * (x - 1964) / 287).)

From the positions of planets in data
111.5 (12.7.111), 687.1 (1.2.687) , 1262.6 (6.8.1262), 1838.2 (9.3.1838)
it can be seen that Jupiter- (Mars) -Earth-Venus-Sun or Jupiter-Earth-Venus-Sun- (Mars) aligns. There are some deviations of Mars but the rest is quite accurate.

The year 1982.1 was calculated - to get a comparable cosine function: 1838.2+ (1838.2-1262.6) / 4 = 1838.2 + 575.6 / 4 = 1838.2 + 143.9 = 1982.1. (Similarly, for example, calculating the minimum between 1262.6 and 1838.2 gives approximately 1550.4 (May 24, 1550), when Jupiter is in opposition to Venus + Earth and Mars is perpendicular to them ...)

Another minimum is about 1838.2 + 575.6 = 2413.8. There is a conjunction of the Sun-Venus-Earth-Mars-Jupiter around 15.9.2413 (slightly earlier than 2413.8).

The symmetry of these positions is not in them, but in what time there are other conjunctions from them. There are slight differences, but in computer outputs they were obvious.

Are there some energy fluctuations associated with these positions that allow that the bodies are aligned in this way? (Attempts to interleave Planet X into opposition of these fluctuations lead to solutions of X about 26900 years, 1104 years, 564 years, 378 years ..., with unclear continuation ...

But it can also be just the inner property of the system - Hallstatt period is derived purely from the impacts of known bodies and the period of 575.6 years resp. also the Vukcevic's period of about 287-289 years are its divisors ...

Neptune beats

Now we show that to explain the Vukcevic envelope cycles the planet Uranus is not needed. (Originally, we considered the 107-110 years that arose by modulating the Uranus period.)

We have shown that curves composed of periods of 115 years and 287 years (whose origin is unknown ....) quite cover well-known climatic periods and the course of solar activity.

But one simple substitution is enough - to use a period Neptune (i.e. N = 164.77 years) and period X = 385.47 years (ratio 3:7) and as beats (1/N plus minus 1/X) come out exactly 2 periods of 115 and 287 years.

The ratio of periods 3:7 ratio is known from the movement of Jupiter's satellites Ganymedes-Callisto. The mutual motion of the bodies creates a cloverleaf.

There are two possible explanations - 385.47 years - is (either)

• 1/ some real period induced by known system (or)
• 2/ some period from planet X

If we exclude planet X we should be able to explain the period according to 1/ or derive i according to 2/ from a more distant planet. Or reject this concept altogether and explain the default (Vukcevic's) periods another way.

Two graphs follow:

First: red abs(50*cos(6.28*(x - 1964)/385.47)+50*cos(6.28*(x - 1964)/164.77))

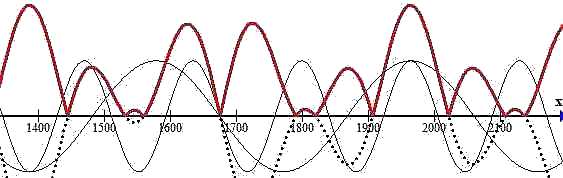
Second: simulated data from movement of X (just assembled to produce a similar graph...) blue - Neptune, green - X, red - abs(blue+green), yellow - difference

Resonance 3:7

An example of linking periods in resonance N:X = 3:7.

 1540 years     1155 years       1540 years     385 years    1155 years
U opos N        N perihel        U conj N      X perihel(?)    N-X(?)	
--------------------------------------------------------------------
                 -920   Pluton=U  -920           -920         -920
                                                 -535  
-150  N=Pluton                                   -150
                  235                             235          235
                        Pluton=U   620            620
                                                 1005  
1390  N=Pluton   1390                            1390         1390
                                                 1775
                        Pluton=U  2160           2160
                 2545                            2545         2545  

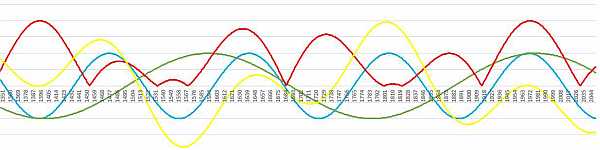
Modulations according to Zharkova

The period of beats of blue and red curves is, according to Zharkova, about 350-400 years. A different course of beats than that of Vukcevic's ones is due to the greater proximity of the curve periods.

But from a very short data set - as Usoskin objected - one can't make predictions for such long periods. Indeed, the conjunction of J-S conjunctions changes, say between 19.1 and 20.5 years (it closes at 60-year intervals ...) The period of the red curve is - based on the analysis according to Kalenda (2019) - about 22.2 years (ie, approximately the length of the Wolf cycle), i.e. less than Vukcevic's 2J.

One of Usoskin's objections is that the extrapolations of the curves according to Zharková does not fit into Sporer's minimum. But the situation around the Sporer's minimum is very changing according to the choice of default periods of the curves. The blue curve is very likely to have a variable period. This greatly influences the course of beats with the red curve (which may have a variable period also…).

Acknowledgment

The majority of the above texts did not arise spontaneously, but from both mail and personal discussions with RNDr.Pavel Kalenda CSc.