The influence of planets on solar activity
| Warren De La Rue, 1815-1889, a British astronomer, chemist and inventor, one of the first creators of a light bulb. In astronomy research he promoted photography, focused on day sun photography.. |
Repelling of sunspots by planets
Effect of Mercury and Venus
The first major work documenting the relationship between planet motion and solar activity is the work of Warren de la Rue, Balfour Stewart and Benjamin Loewy (1872). Based on Carrington observations of about 400 sunspot groups and another 400 groups documented at the Kew Observatory they have stated several rules for motion of the spots.
Balfour Stewart| Balfour Stewart, 1828-1887, Scottish Physicist, Head of the Kew Observatory. He dealt with radiation, especially radiant heat. |
From their surveys (which have started already in 1862-1866) the maximum spots adheres to the side of the sun that is opposite to the nearby planet. This is fulfilled reliably for Venus, with similar schemes apparent for Mercury - for Jupiter, the relationship was not reliably proven. (The aim was to develop a wider treatise, but it did not happen). Similar observations were made on a larger scale by M.Birkeland in 1899.
Here are the first questions .... Is this expression gravitational, magnetic, electrical or other essence? Do nearby planets act on the sunspots so that they "just repel" them or they affect the overall solar activity (the activity of the entire Sun)?
Magnetic fields of planets
Magnetic fields of planets differ. The outer large (gaseous) planets have very
strong magnetic fields: Jupiter and Saturn are approximately dipole,
Uranus and Neptune fields are more complex.
Even the Earth's magnetic field is considered to be relatively strong,
it is approximately 100 times stronger than the magnetic field of Mercury.
The fields of Venus and Mars are at the limit of measurability -
for Venus it is caused by very slow rotation.
As regards the observed repeling of the spots, it is therfore difficult to suspect
Mercury and Venus of magnetic influence !?
Mercury and Venus
The Mercury-Venus conjunctions occur with an average period of approximately 144.57 days, with shorter intervals (126-131 days) and longer intervals (153-158 days) alternating frequently. For example, in 1989-1991 (Lm, Lv and Le are heliocentric longitudes).
Distance Days Year Date Lm Lv Le ----------------------------------------------------------------- 0,43 158,00 1989,27 1989 Apr 4 AD 14.8 14.6 194.9 0,36 131,00 1989,62 1989 Aug 13 AD 224.7 226.0 320.9 0,40 147,00 1990,03 1990 Jan 7 AD 99.2 100.2 107.1 0,43 157,00 1990,46 1990 Jun 13 AD 351.3 351.7 262.4 0,35 127,00 1990,80 1990 Oct 18 AD 196.3 196.4 25.0 0,42 153,00 1991,22 1991 Mar 20 AD 81.3 80.2 179.5 0,42 154,00 1991,64 1991 Aug 21 AD 327.2 327.3 328.1 0,35 126,00 1991,99 1991 Dec 25 AD 169.6 169.9 93.3
View from the Earth
Earth meets Venus on average every 583.92 days = (V, E).
E.g. in the years 1984-1994, the following days are Mercury and Venus
(seen from Earth) hidden behind the Sun.
Configuration MV - E (max inaccuracy approx 10 dg)
Distance Days Year Date Lm Lv Le
-----------------------------------------------------------------
1984,48 1984 Jun 22 AD 88.5 95.9 271.5
1,61 588,00 1986,09 1986 Jan 31 AD 310.3 318.3 131.6
1,54 563,00 1987,63 1987 Aug 17 AD 132.7 140.5 324.3
1,63 594,00 1989,26 1989 Apr 2 AD 4.7 11.4 192.9
1,55 565,00 1990,81 1990 Oct 19 AD 199.8 198.0 26.0
1,61 589,00 1992,42 1992 May 30 AD 66.0 60.9 249.9
1,59 581,00 1994,01 1994 Jan 1 AD 277.9 272.9 101.4
There is a doubt ... Do the planets operate according to the De La Rue rule really just to one side of the Sun, or they can - as happens during tidal action - to affect both (opposite) sides of the Sun? In the first case, the MV - E configurations would have more spots towards the Earth (than in the opposite direction).
Fernando Sanford| Fernando Sanford, 1854-1948, American physicist. He dealt with Earth's electricity. |
Comparison of conjunctions and oppositions
The answer to the last question was dealt with by Fernando Sanford. He compared (for the period 1918 to 1932) the visibility of the spots with the frequency of the conjunctive cycles of Venus and Earth. Observed (in the 14-year period) the most spots (on average 714). at the time of opposition V-E and on the contrary least spots (405) at the VE conjunctions.
Sanford's observation was later reviewed - for a longer period (ca. 1875-1975) and including Mercury - by a trio of Czech scientists: Kopecký, Link, Mayer. They confirmed that the number of spots between the oppositions and the conjunctions of planets differs significantly, the planets have (when working together) a negative effect on the spots.
Annie and Walter Maunder| Annie Rusell Maunder , 1868-1947, a Edward Walter Maunder , 1851–1928, couple known for their contributions to observing the Sun and its activity.. |
Effect of the Earth
At the turn of the century, the Earth also entered the game (started by De La Rue in 1872).
Mathematician Annie R.Maunder succeeded in establishing (1906-1907) similar rules for the Earth
as previously observed for Venus and Mercury.
Even the Earth has a negative effect on spots -
the number and size of spots diminishes on the visible hemisphere.
This result was subsequently confirmed by other researchers -
Robert John Pocock supported Maunder's claim based on his observations from 1902-1917.
In our previous example of configurations Venus-Mercury-Sun-Earth the spots "pushed" towards the Earth are "repelled" (according to Maunder) back by the Earth...
Doubts about the action of the Earth
The Earth differs from the Mercury and Venus in one thing - it is also an object, from which we observe these phenomena. We see some things from the Earth distorted and so there doubts appeared. In 1932, Dutch astronomers Marcel Minnaert (1893-1970) and A.J.M.Wanders showed that a larger number of spots originating in the Eastern Hemisphere of the Sun (ie further from the actual conjunction with the Earth) can be only apparent.
The phenomenon was later analyzed in detail by Czech scientist Link. He showed, that the asymmetry of the visibility curve described by Minnaerth is in the center of the solar disk negligible, but the number of extinct spots here is still larger than the number of defects. He confirmed that Maunder's conclusions were correct.
Tidal action
Mercury and Venus
Venus is heavier than Mercury and revolves on a circular orbit. Mercury orbit is considerably eccentric. After conjunction with Venus Mercury gets an additional impulse (Venus decreases moment of Mercury movement and it starts move like it was nearer to the Sun.) Before conjunction is Mercury on contrary decelerated. Similar phenomena cause in case of satellites of Jupiter, Saturn and Uranus resonant motions. But Mercury and Venus do not show such a resonant binding. Conjunctions M-V appear also when Mercury is in aphelion, e.g. at end of year 1993 and near half of year 1999 (after c. 5.54 years ~ W/2, this cycle is not permanent, it disappear after 9 or 10 occurrences replace by new, phase shifted cycle…):
(Interval) Conjunction M-V Mercury in aphelion
------------------------ --------------------
1993.989 1993.986 1994.227
( 0.381) 1994.370 1994.468 1994.709
( 0.433) 1994.802 1994.950
...
1998.718 1998.805 1999.046
( 0.433) 1999.150 1999.286
( 0.383) 1999.533 1999.528
Synchronization Mercury with Venus can be seen only in combination with rotation. Solar day on Mercury lasts (M,Mr) = (87.969, 58.646) =175.938 days, on Venus (V,Vr) = (224.8008,-243.1)=116.796 days. So it holds approximately:
(M,Mr)/(V,Vr)= 3/2
Solar day on Venus is 1.5 multiple of solar day on Mercury. (To keep periods exactly in this ratio some small changes are necessary, e.g. to shorten mean rotational period of Mercury by 2 hours).
Mercury, Venus and the Earth
The period with which Venus meets Earth, 583.92 days = (V, E) fits approximately to the sequence with which Venus meets Mercury, 144.57 days = (M, V). Four cycles 4 * 144.57 days give 578.26 days.
In the view of the Earth, we see this situation differently: The Earth meets Mercury on average every 115.8775 days = (M, E), and five of these cycles are 579.3875 days. On the other hand, the fifth of the Venus-Earth cycle is (V, E) / 5 = 116.7840 days.
Ratio (V,E) / (M,V) / 4 = 583.9214/ 144.5662 / 4 = 1.00978 (<1%), ratio (V,E) / (M,E) / 5 = 583.9214/ 115.8775 / 5 = 1.00783 (<1%).
The period (V, E) is approximately followed by the asteroid Toro (T_orbit = 1.6 years, T_libration 150 years). In perihelion - Toro is close to the Venus orbit, in aphel - is behind orbit of Mars.
The beats (M, E) with (V, E) / 5 are about 40.87 years. So-called Chandler's Earth magnetic pole movement also follows approximately 40 years period. For 40 years, Mercury turns around 255 times.
Zdeněk Kopal| Zdeněk Kopal, 1914-1993, Czech astronomer, astrophysicist and mathematician. He dealt with variable binary stars, the moon and the inner planets of our system. He pointed to the tied rotation of Venus. |
Bound rotation of the planet Venus
In the Solar System we find many ratios close to the ratios of small integers. Such cases usually mean either a random phenomenon or resonance. The fact that the resonance ratio is not realized precisely is then usually the work of other contexts - change in the orbit of bodies, motion of perihelions, inclination of tracks, etc.
The period of rotation of Venus in relation to the Venus orbital period (ie "day" on Venus) makes (V, Vr) = (224.7008, -243.1) = 116.769 days (Vr is given a negative sign - the rotation of Venus is opposite ...)
In this case (V, E) / 5 = 116,784 days and thus (V, E) / (V, Vr) / 5 = 116.784 days / 116.769 days = 1.00013 (<0.2%). In every conjunction (V-E), Venus directs "the same face" to the Earth ...
This relationship is written in the form of resonance 1/Vr-5/E+4/V = 0.
The influence of Mercury
The influence of Mercury is sometimes neglected, because its duration is very short in comparison with the solar cycle length (K.D.Wood).
The influence of Mercury was dealt with in detail by Bollinger (1960). E.K.Bigg explored (1968) the statistical reflection of Mercury's motion in solar activity data (observing the speed of tidal force change) and showed that Mercury's influence in the data of solar activity appears (and depends on the phases of Venus, Earth and Jupiter). The action of planets is the trigger of the main cause of activity. (G.A.J.Ferris).
Carl-Gustaf Rossby| Carl-Gustaf Arvid Rossby, 1898-1957, American meteorologist of Swedish origin. He explained the movements in the atmosphere by means of fluid mechanics. He described the jet air flow along the parallels on the Earth in the direction of rotation and later - in collaboration with the German scientist Hans Ertel (1904-1971) - the so-called Rossby Waves. |
Rossby's waves
Venus day (116,769 days) and Mercury (175,937 days) are in the ratio of 2: 3, the day on Mercury is twice its period (87,969 days).
Roosby's waves are waves in the atmospheres and oceans on the planets. It is related to rotation of planets and significantly affect climatic phenomena. Recent research has shown that similar waves can be observed in the sun.
I.R. Edmonds (2015) observed the reflection of 88 daily and 176-day periods in data of solar activity. He shows that some Roosby waves can be described by simplified formula T (q) = 25.1 q / 2 [days], where 25.1 days is the equatorial period of the photosphere on the Sun. For q = 7, T (q) = 87.85 days and for q = 14 T (q) = 175.7 days. The influence of Mercury was observed only for non-overlapping (discrete) parts of the cycle (episodes). The exact phasing of the influence of Mercury with the phenomena on the Sun could not be confirmed.
Tidal forces
The tidal action of planets on the Sun is proportional to m/r^3, where m is the mass and r distance of the planet from the Sun.
Jupiter Venus Mercury Earth Saturn Mars Uranus Neptune
-------------------------------------------------------------------------------------------
(H.M. Losh) 2.30 2.16 1.24 1.00 0.11 0.03 0.019 0.001
(K.D. Wood) 2.28 ± 0.32 2.17 ± 0.04 1.15 ± 0.65 1.00 ± 0.05 - - - -
Only the first 4 bodies in the table are considered to be significant, the influence of others is usually neglected. Considerations on the interaction of planets are often reduced to the conjunctions of Jupiter with Venus in opposition to Earth or the conjunction of Jupiter with Earth is in opposition to Venus.
Bendandi (1931) observed that the tides of Venus, Earth and Jupiter create oscillations with a period of 11.07 years.
The usual tidal effect is such that it acts the same on the facing and averted side (as we know from the ocean movement on Earth due to the tidal effect of our moon). But it can be different on the Sun ....
Karl D. Wood|
Karl Dawson Wood, 1898-1995,
an American engineer, a specialist in applied aerospace, thermodynamics and rocket control.
He also dealt with aerodynamics - design of aircraft and spacecraft. He showed that alignment of planets J-V-E with the sun (with a period of 11.07 years) proceed synchronously with the solar cycle over the 1500 years covered by data of Justin D.Schove. |
Tidal fluctuations
Doubts about the possibilities of tidal power led to new theories. The authors prove that the inner planets act on the Sun with comparable forces to the forces of outer planets and that tidal fluctuations can greatly affect the acceleration and "jerk" (indicator of change of the acceleration ) of the Sun.
R.M.Wood and K.D.Wood created (1965) a dynamic model (for all planets except Mars and Pluto). From the average period of bodies they derived a period of 11.08 years. According to C. J. Bollinger (1967), the tidal action of the planets Mercury, Venus, Earth on the Sun influences changes in winter temperatures on Earth. He deducted periods of 11.19 years and 111.9 years.
Takahashi (1967) examined the influence of the second power of tidal power. Then (1968) he pointed out that rapid changes in tidal power ("jerk") are the result of a sequence of (multiple) or sharp drops in quadratures of (tidal) planets.
K.D.Wood then (1972) has documented that so-called "tidal fluctuations" correlate with the occurrence of sunspots.
According to the theory of N.Scafetta (2012), the Sun can amplify tidal power by nuclear fusion. P.Kalenda (2018) considers tides as an auxiliary mechanism for transmission of rotational moments. He tried to express the total effect of tides using gravitational "dipoles".
Robert M. Wood|
Robert M. Wood , -,
American projects manager in aviation engineering. He dealt (together with his son)
with problems of UFO and with hypotheses about extraterrestrial civilizations.
Compared the periods of solar activity with the synodic periods of planetary motion. |
Detailed comparison
To assess the correlation we compare the extremes of the planets Jupiter, Venus and Earth to the actual observed cycles of activity.
Among all the differences, the extremes between 1770 and 1800 seem to be the most critical. The J-V-E alignment occurred in 1771.0, 1779.8, 1791.8 while extremes of activity were observed in 1769.7, 1778.4, 1788.1. Here, for example, difference 1791.8-1788.1 = 3.7 years, ie more than 2 conjunctive loops of Venus-Earth. We conclude that the coincidence of solar activity cycles with V-E-J conjunctions is just random. It is only a match of periods and a seeming synchronization.
Sub-alignments (for example, Venus-Jupiter, Venus-Earth) occur more often than the extremes of activity. In some cases, such as 1958,1960,1962, we could try to explain this by multiple maxima of activity ... But number of "potential maxima" is greater than can have some reflection on the Sun...!
For the above reasons, ideas have come to integrate tidal influence. Jean-Pierre Desmoulins (1989-1995) has attempted to calculate and display the graph of the summary impact of tides. See Jean-Pierre Desmoulins. The period of cycles appears to correspond in the long run to the period of solar cycles, but the amplitude of cycles stagnates at approximately the same level.
Another idea is that the tiles act depending on the orientation in space (e.g., relative to the barycentre). But attempts to find a mechanism that would preserve the "good" cases and correct the "bad", failed.
Artur Schuster| Artur Schuster, 1851-1934, a British physicist of German origin, engaged in radiation (optics, spectroscopy, radiography) and applications of harmonic analysis in physics. He developed the technique of periodograms to reveal frequencies in time series and applied it to the earthquakes and solar activity. |
The influence of Jupiter
The solar cycle has been from the beginning of observation - due to its period not too distant from the period of Jupiter - associated with the influence of Jupiter - Rudolf Wolf, R.C.Carrington (1859). F.B.Edmonds (The Sun-Spot Period, 1882) suggested (based on observation of activity in 1766-1799), that periodicity of creation of spots is related to the location of the planets Jupiter, Venus and Earth.
Artur Schuster (1911) confirmed, that the relationship between the appearance of the spots and the position of Jupiter is indeed nonrandom. Based on daily photos of spots from 1874-1909 he deduced, that Jupiter (as well as Venus and Mercury) also affects existence of spots.
The distance of Jupiter from the Sun varies depending on the third power of the ratio (1+eps)/(1-eps) which is 1.337. The tides in Jupiter perihelion are about one third bigger than in aphelion ... see above K.D.Wood: (2.28 + 0.32)/(2.28 - 0.32) = 1.326. Tidal peaks therefore concentrate around Jupiter perihelion.
The conjunctions of Venus-Jupiter advance (unlike the above described MV-E conjunctions)
- thanks to Venus' almost circular trajectory - with great regularity.
The spacing is about 236-239 days.
The average conjunction period (V, J) = 236.9919 days = 2 * 118.496 days coincides with periods
116.769 days, ie (V, Vr) and 115.8775 days, ie (M, E) (error<2.5%).
The statistical research of Jupiter's influence on the Sun was carried out between 1988 and 1991 by Timo Niroma.
Precessional action
Arthur G.Webster| Arthur Gordon Webster , 1863-1923, American physicist. |
Precessional action of planet on the Sun
The influence of the planets on the creation of sunspots was dealt with in several works (1930-1947) by W.A.Luby. According to his theory, the power action of planets on the Sun intersects with the rotation of the Sun, causing a "precession". The size of the precession counts according to the formula in Webster's book "Dynamics ...", the function decreases with the third power of distance.
William A.Luby| William Arthur Luby , 1872-1947, American mathematician of Irish descent. He focused on algebra and geometry, and he liked astronomy. |
W.A.Luby considers the influence of the planets Mercury, Venus, Earth, Jupiter, and Saturn. For each planet it assumes 2 maxima and 2 minima effects, the effects is solved graphically. He notices the operation of Jupiter and Saturn (conjunctions, quadratures). He deduce the period is 112.5 days, 11.2 years and 22.5 years from Venus, Earth and Jupiter.
The influence of the outer planets on the Sun
Paul D. Jose| Paul D. Jose, a scientist active in Aerospace Research, known for his observation of motion of the sun around the barycentre. His work inspired many other scientists. |
Periods of repeating patterns
The positions of the external planets of the solar system are repeated with a period of about 180 years, more precisely about 178.7 years (Jose 1965). This period is one of many possible approximations of common synodic multiples of period of outer planets.
R.M. Wood's (1975) compared the synodic periods of the planets with solar activity periods.
Jupiter and Saturn make in conjunction with Uranus a period of about 139.0 years = 7 * (J, S), in conjunction with Neptune, about 218.5 years = 11 * (J, S). The period 178.7 years = 9 * (J, S) makes three loops with a return to a similar configuration (Gary J. Morris, 1997).
An analysis of the synodic periods of the outer planets comes with two basic cycles: A = 178.95 (177.50-181.00) and B = 317.75 (317.45- 319.55), followed by their linear combinations (2A, A + B, 3A, 2A + B, 3A + B, ...) (357.90, 498.50, 536.85, 677.45, 856.40, ...). The period of about 500 years is supported by the synodic period (Neptune, Pluto), 676 years is the Mayan period of 13 calendar rounds (13*52 years, "oxalajuj tiku") and 855 years is twice the Babylonian period (427 years).
In a number of periods over a thousand years, the Mayan refer periods 2582 years and 5125 years. Fairly accurate is the period c.2224.10 years (double the G.L.Siscoe period, 1020-1030 years), and c.2403.05 years (the period observed by I.Charvátová) and especially their sum of 4627.15 years.
However, we can never find any reliable pattern (J. Čech, 2007). The new patterns emerge similarly when moving to a higher resolution level like higher numbers in chain fragments ... This pitfall recalls the introduction of a 12-tone system in music. In both cases it is a good approximation to real-world relationships with a simplest system (180 years < 4627 years, 12 tones < 53 tones, etc.).
Theodor Landcheidt| Theodor Landcheidt , 1927-2004, German (amateur) climatologist. He dealt with the analysis and the possibility of predicting various natural phenomena - extremes of solar activity, occurences of El-Niño, etc. |
Changes of torque
Some theories derive solar activity from changes in angular momentum of (outer) planets. The maximum moment is at the time of conjunction of planets (the center of gravity is shifted from the Sun to the planets) The minimum moment is at the time of the opposition (the center of gravity is near the center of the Sun).
In both cases, the torque change is minimal and therefore a minimum activity is expected. The maximum activity should be about 60º at the distance of the planets, ie 2 maxima per 1 minimum!? (According to these assumptions, the minimum activity would also be around the year 1992 - which did not occur).
P.D.Jose (1964, 1965) observed the rate of change in the angular momentum of the sun and deflection of the Sun by the planets Jupiter and Saturn with respect to the barycentre.
According to Theodor Landcheidt (1983), the "torque" changes are the changes T = dL/dt of angular momentum (torque) L and "impulses of torque" (IOT) changes d2L/d2t. In 1988, he found an IOT signal in the time series of solar rotations (Mt.Wilson).
James Shirley|
James Shirley ,
American scientist (NASA, Jet Propulsion Laboratory),
co-author of the Encyclopedia of Planetary Sciences.
He deals with the movement and rotation of the Sun, solar activity, the atmosphere of Mars, Jupiter's moon Europa, geophysics, seismology, ... He pointed to a certain correlation of the occurrence of the earthquakes, the solar cycle and the moon's motion. |
J. Shirley (1990) analyzed in detail instrumentally acquired data of solar radiation intensities of different frequencies. He deduced that the data do not contradict the results of previous observations (De La Rue, Stewart a Loewy (1872), Schuster (1911) or Bigg (1967),...).
J. Shirley confirmed there are frequencies in the solar spectrum that could be induced by planets - such as the impact of Mercury and Venus, the simultaneous action of the Earth and the outer planets, However, he distinguishes the impulses (IOT, d2L / d2t) and tidal forces. He ruled out that the observed manifestations on the Sun could be part of the tidal forces.
Speed and acceleration of the Sun
The speed of change in solar acceleration was examined by K.D. Wood and R. M. Wood (1965). If we focus on the influence of the outer planets than there is (despite the variation in extremes, about 15-22 years) behind everything still period (J, S) ~ 19.86 years. Observation of the acceleration of the Sun caused by the outer planets does not seem to lead directly to the 11-year cycle seen in solar activity. The speed and acceleration cycles correlated with Solar activity can be derived only in combination with inner planets.
A critical analysis of the different types of forces and derived accelerations is in the work of the authors D.K.Callebaut, C de Jager and S.Duhau (2012).
Direction of the barycentre
Theodor Landscheidt pointed out that there are some differences in solar activity in the direction of the Sun to the barycentre and in the direction of the barycentre.
Theodor Landcheidt (1976) observed the relative position of the Sun, Jupiter and the center of gravity of the solar system (barycentre). He compared the direction of the solar storms in 1951-1956 and deduced that their larger part (about 2/3) takes place in the direction of the barycentre.
A similar principle (combined with tidal theory) examined (independently of T. Landscheidt) also Czech geophysicist Pavel Kalenda.
Ivanka Charvátová| Ivanka (Jakubcová) Charvátová , 1941, Czech geophysicist, focuses on the movement of the Sun, its relation to solar activity and its impact on climate phenomena on the Earth. |
Deflection of the barycentre
Alexandre Dauvillier - French scientist associated higher solar activity with a greater distance of the sun from the barycentre..
The theory of harmonic and chaotic arrangements was elaborated by the Czech geophysicist I.Charvatova.
According to her theory - solar activity decreases at times when the ordered (harmonic) movement of planets Jupiter and Saturn is disturbed by other bodies. Because the greatest known disorders are caused by the outer planets of Uranus and Neptune, we deduce, that solar activity decreases at the moment of their conjunction (chaotic periods). So far, it is consistent with classical moments of momentum theory.
In chaotic periods - with variable longer cycles (ie around the conjunctions U-N:r. 1136, 1307, 1479, 1650, 1821, 1992,…) is Jupiter in the aphelion during solar peaks. (that is, the Sun-J and Sun-U-N center of gravity is further from the Sun)
On the contrary, during ordered (harmonic) periods - with short 10-year cycles (ie in the wider neighborhood of oppositions U-N: 1051, 1222, 1393, 1565, 1736, 1908,... is Jupiter at perihelion during solar peaks (that is, the Sun-J center of gravity is closer to the Sun).
The possible connection between the Uranus-Neptune conjunctions and the long-term minima of solar activity was demonstrated also by Geoff J. Sharp (2013).
Average cycle length and Jupiter
In the period 1848-1907 the cycle length approximates to Jupiter's orbit:
Period Beats [years]
(1829,90...1883,90) ( 54,00, 59,31) => 120,63
(1837,20...1894,10) ( 56,90, 59,31) => 280,06
(1848,10...1907,00) ( 58,90, 59,31) => 1704,18
(1860,10...1917,60) ( 57,50, 59,31) => 376,83
(1870,60...1928,40) ( 57,80, 59,31) => 454,07
(1883,90...1937,40) ( 53,50, 59,31) => 109,23
190-year period
"Deification" of the 180-year period gradually met with criticism and new methods of solar spectrum analysis. Already in 1973 T.W.Cole derived a period of 190 years. Similar results have been made in recent years by several other scientists - Richards (2009), J. E. Solheim (2013). S.K.Solanski (2004-2005) reconstructed solar activity 11,000 years back.
Research is based on an analysis of the "O-C" deviations resulting
from timing of solar minima:
t(min) = 1755.5 + N * 11.06 + δ(O-C)
Source
----------------------------------------------------------
T.W.Cole (1973) 190 years
Rogers, RichardsAndRichards (2006) 188 years (+-38 years)
J.-E.Solheim (2013) 190 years (+-7 years)
Quadratures of planets and solar activity
The definition of the "quadrature" of two bodies (similarly to the definition of conjunction and opposition) differs in geocentric and heliocentric astronomy. We will hold the heliocentric view and understand as the quadrature of two bodies the moment when the angle of Planet1-Sun-Planet2 is right, ie when the difference (heliocentric) of the planets is 90 degrees.
Quadratures of the outer planets
The following three images represent the position of planets at the time of greatest extremes (maxima) solar activity of the last three centuries ....
23.5.1778
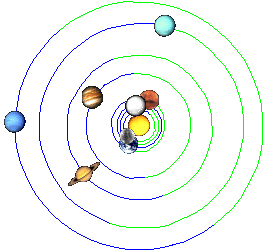 30.6.1947
30.6.1947
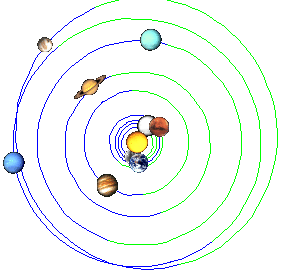 22.11.1957
22.11.1957
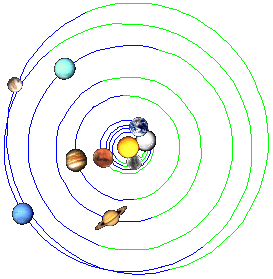
We see that the Uranus and Neptune planets have a right angle.
At the same time, these positions are preceded (in advance of 1-2 years) even
by the quadratures of the planets Jupiter and Saturn
(1778.4-1777.4 = 1.0 years, 1947.50-1946.47 = 1.03 years, 1957.90-1956.17 = 1.73 years).
Five of the ten largest sunspots in 1874-2014 were observed in 1946-1951.
(The positions of 1778 and 1957 are similar, covering a 178-180-year cycle of outer planet positions).
It offers to find a function of contributions of individual pairs of planets (ideally using vector products, which are proportional to the sinusoidal function of the angle and thus acquire the highest values under the action of two forces in the perpendicular direction) ...
But the thing is not so simple. The highest extreme of solar activity in the last millennium (according to the values of Justin D.Schove) occurred in 1372. The angles of the observed planetary pairs (Jupiter-Saturn, Uranus-Neptune) are here quite precisely 120 degrees !?
01.07.1372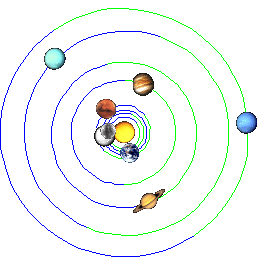 John H. Nelson
John H. Nelson
| John H. Nelson , 1903-1984, American radio wave propagation analyst. He described some correlations between planetary positions and disturbation of radio signal and managed to predict some extremes of it. Due to the nature of the research, he was criticized by the scientific community. His work was recognized by astrologers, though he did not belong to them. |
Nelson's theory
John H. Nelson watched the conjunctions and quadratures of the planets in connection with radio transmission of signals and the occurrence of solar radio storms. He discovered (1951) greater interference of the radio signal at times when angles included by some planets were multiples of 90 degrees (aspects 0, 90 and 180 degrees).
Interference at these times may have been caused by an increase in solar activity. But Nelson did not claim that the planets controlled the processes on the Sun - he "only" tried to prove he was capable to predict magnetic disturbances, and to change radio frequencies so that they do not happen to interrupt signal transmission.
An example of observed signal interference is the date 01.10.1961 (planets JSM-V # NR-E):
To get closer to the Nelson observation logic, let us introduce the following definitions:
- Two planets are "in a cross" when they are in conjunction, opposition or quadrature..
- Two planets are "in compliance" when they include an angle of 120 degrees (multiples of 60 degrees).
It is important to consider::
- Cross Jupiter-Saturn and cross of Mars with Jupiter or Saturn.
- Cross of Venus, Mercury or the Earth with Jupiter, Saturn or Mars.
- Some of the inner planets are near Jupiter or Saturn in the cross.
Nelson predicted the solar storms:
12.11.1960
 31.08.1962
31.08.1962
And further (are important):
- Compliance Jupiter-Saturn including compliance Jupiter-Saturn-Mars
Nelson pointed to the drop of interference at the beginning of 1948 with an angle (J-S) of 120 degrees.
Smoothed extreme solar activity is given to be on the year 1947.5. At the beginning of 1948, however, a short-term decline occurred. (Wolf's quarterly numbers 1947: 126, 172, 172, 136, 1948: 97, 177, 148, 127)
According to J.H.Nelson, radio signals of better quality, when Jupiter angle with Saturn make multiples of 60 degrees. In the days 26-27 March 1948 with outer planets at Lj = 258, Ls = 142, Lu = 86, Ln = 192) the extreme of the triangle alignment of the index occurs. The straight line formed by Jupiter and Uranus divides by Saturn and Neptune into 60-degree sectors. (A few days later, the system is symmetrical, including the inner planets.)
10.4.1948
In connection with the planetary layout of 23.02.1956 (PJE # SRM-V) Nelson also became interested in Pluto..
The Nelson's method was later adopted by J.H. Clark and expanded - besides Pluto - also to Uranus and Neptune.
However, the extremes mentioned in the previous paragraphs do not seem to fit into Nelson's scheme: maximum r.1372 and maximum end of 1957. In these cases, "compliance" (angles of 120 dg) should lead to lower activity, but on the contrary, the activity is extreme !?
Romanchuk's forecasts
P.R.Romančuk (University of Kiev) compiled in the 1960s of the last century - for the purpose of forecasting of solar activity - a function to which entered the longitudes of the planets and also their differences. Hence activity was decided by mutual position of the planets (conjunctions, quadratures, ...). He constructed a special empirical "function of action" the calculations included Jupiter, Saturn, Venus and Earth.
Romanchuk's functions were not hereafter used, because their calculation was quite demanding, but the forecasts did not achieve greater accuracy than other (statistical) methods..
Blizzard's observations
J.B.Blizzard (1965) observed the rate of change in tidal power (for particle events on the Sun) and the resonance sequence of planetary conjunctions. Subsequently, in the extensive treatise (1968) on solar eruptions and proton phenomena, he has attempted to prove that they are preceded by conjunctions of the planets.
Mars and Jupiter
Planet Mars seems to be completely meaningless by
its size, but it appears in time of solar maxima and proton
events in conjunction with Jupiter more often, than would be expected
from an accidental distribution.
It applies, for example, to proton flares:
1.9.1859, 28.9.1870, 10.9.1908, 9.8.1917,
7.3.1942, 25.7.1946, 4.5.1960,
28.1.1967, 10.4.1969.
Proton eruption 7.3.1942
But also for example large sunnspots (M.A.Ellison), of years 1946 and 1951, follow each other at interval of 2 conjunctions Mars-Jupiter.
Giant sunspot 27.7.1946 Giant sunspot 25.5.1951

Mörth-Schlamminger's theory
H.T.Mörth (United Kingdom) and L.Schlamminger (Germany) published in 1979 (in collection Solar-Terrestrial Influences on Weather an Climate) article PLANETARY MOTION, SUNSPOT AND CLIMATE. According to their observations, the largest amplitude of solar activity correlate with 90 ° longitudinal angles.
Their function is based on a combination of pairwise external conjunctions planets, especially Jupiter-Saturn and Uranus-Neptune. It is written here: „The long period peak amplitude variation appears to be associated with the angular separation of Uranus and Neptune, greatest amplitudes at angular separation 90°, smallest amplitudes near conjunction and opposition“.
They provide graph of function |Ln-Lu| + |Ls-Lj| (where Lx are "adjusted" heliocentric longitudes of planets) for period 1750-2000, that cover progress of solar activity – e.g. estimated maxima from the graph are around years 1780,1840,1870,1960. Based on these assumptions they derive cycle ((J,S),(U,N)) = 22.46 years. The adjustment of longitudes is based on: L = L-90 for 90 < L ≤ 180 degrees!?
But Mörth-Schlamminger period 22.46 years, respectively. 11.23 years seems to be too long. In the long run, it does not fit into Schove's extremes, the functions are diverging with the course solar activities. Regularity after several centuries (for example, before 1540 and after 1950) ceases to exist (or overflows to the opposite polarity). Some deviation also occurs around year 1780.
Contrary to real activity, the theory is also in 1989-1990.
Four of the ten largest spots of 1874-2014 appeared in 1988-1990.
At the same time, this marked activity peak occurred when aligning (known)
outer planets into one line!
06.08.1989
| Ian R.G. Wilson , [vilzn], Australian astrophysicist and climatologist, author of several treatises on the "quadrature effect" - in motion outer and inner planets. He also deals with long-term cycles of solar activity, with the Moon, and so on. |
Transitional periods
Jozsef Garai (2009) distinguishes regular and irregular cycles, regular are those that proceed with the specified period given by syzygies (conjunctions and oppositions) of Jupiter and Saturn. Periods with irregular cycles will be called "transitional". Transitional periods are also referred to as periods of "phase collapse" or "phase catastrophe" (Wilson, 200?).
Close proximity
Depending on the location of the bodies, we can distinguish between two types of quadrature:
- 1. Before coupling bodies (faster body at the back),
for J-S eg 1778, 1837, 1958, for U-N, 1778, 1947, 1958. - 2. When the body is collapsing (faster body in front),
for J-S eg 1727, 1947, for U-N 1870.
The high extremes of solar activity between 1727 and 1837 are closely preceded by quadratures of Jupiter-Saturn (1727.50-1727.39 = 0.11 years, 1837.20-1836.99 = 0.21 years).
29.6.1727
 11.03.1837
11.03.1837
| Gnevyshev, M.N., [] 1914-1992, Russian scientist, founder and director of Kislovodsky Sun Station of the central astronomical observatory. Significantly affected the development of solar physics in the second half of the 20th century. His scientific work also intervenes into medicine, studying, for example connections of solar activity, geomagnetism and the incidence of myocardial infarction. |
11-year period?
Wolf's 11-year period is based on long-term averages. However, in some periods, activities with a significantly lower period are taking place. in the period 1905-1958 the process of extremes of activity corresponds quadrature procedure - 5 cycles gives (measured between maxima) an average of 5x10.18 years, quadrature covers 5x10.04 years.
There are indications(the Gnevysev-Ohl rule) that an extreme around 1797 is missing (see below). At Maunder's minimum, long cycles (up to 14 years) are expected. However, if it appears that some of the maximum is also missing here (eg y.1669), it would reduce the average period to under 10.5 years ...!?
Not quite clear is the situation of approx. 80 years after 1796, around 1877 - there is no violation of the Gnevysev-Ohl rule, but the length of the cycle between maxima of 1870.6-1883.9 is almost 14 years.
Usoskin, Ilya| Usoskin, Ilya, physicist working in Finland. Author of a long series of scientific publications in the field of solar physics and physics of cosmic radiation. |
Missing maximum y.1796
It seems like maximum of the year 1796 in data of solar activity „drops out“?!
-
From the analysis of phases of the double solar cycles (1871-1981)
the following sign of individual cycles were derived:
Note the same sign in cycles 4-5 a 11-12.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 + - + - - + - + - + - - + - + - + - + - - Regular change of cycle signs is known as the "Gnevysev-Ohl Rule".
- I.Usoskin has also pointed out (in y.2001), that the cycle No.4 (ca.1788-1805) may be composed of two cycles (ca. 1788-1796, 1796-1805) - see also: I.Usoskin (pdf, 2009)
- It was proposed to reduce the cycle numbers from 1,2,3 to 0,1,2 and add the missing cycle number 3.
- The year 1795 was also identified as the beginning of 80-year secular cycle (in work of H.C.Willett). See Gleissberg's 80-90-year cycles.
Planets Jupiter, Saturn and Uranus were near their perihelia in the year 1797. Consider the position of the planets in the year 1796, for example 19.August 1796 (when also Mars was near its perihelion):
There were only 2 such years on interval 0-2100 (with precision 10 dg) about 1090 years apart...(Program skips 100 day after an event found - this is why we see here 2 rows for each of these years ...)
J Jp S Sp U Up N Np
706,05 4,41 ( 11,53) 75,01 ( 84,93) 169,74 (170,33) 356,59 ( 30,47) 706 Jan 14 AD
706,38 15,35 ( 11,51) 79,55 ( 85,03) 171,27 (169,98) 357,32 ( 32,41) 706 May 14 AD
1797,41 5,38 ( 13,85) 93,33 ( 91,95) 164,69 (169,11) 222,35 ( 40,70) 1797 May 27 AD
1797,74 16,37 ( 13,85) 97,83 ( 92,04) 166,24 (168,74) 223,05 ( 42,48) 1797 Sep 24 AD
And the cycle 699-714 (i.e. distance of extremes, similarly to 1788-1805) was also (in the series of extremes according to J.Schove) relatively long!
Pairing extremes and quadratures
We will try to pair cycles to the J-S quadratures. For the period 1905-1958 we get:
1905.96 (1.04) 1907.00 1916.53 (1.07) 1917.60
1926.81 (1.59) 1928.40 1936.27 (1.13) 1937.40
1946.47 (1.03) 1947.50 1956.17 (1.73) 1957.90
The maxima of cycles are lagging here the quadratures on average by about 1.27 years. But we chose periods the strictest pairing. Including other regular cycles we get greater average delays (for the period 1600-2000, about 1.7-1.8 years).
A typical example of an average distance would therefore be maximum 1957.90, which is behind the 1956.17 quadrature by 1957.90-1956.17 = 1.73 years. Given the average length (J, S) = 19.86 years it is 31 degrees. Thus, at the peak of activity, the Jupiter-Saturn angle is on average rather at 60 or 120 degrees. So Nelson's theory is not still out of the game !?
Verification of angles
Observations so far may be random. We need to know if there are some angles of Jupiter-Saturn in extremes of activity really more significant or not.
In the "J-S" column we will give the exact angle, in the column "Angle" this is rounded to a 30 degree raster. The column "Factor" has value = Angle / 30.
For the period 1917-1947 we get:
Interval Days Extreme of activity J S J-S Angle Factor
--------------------------------------------------------------------------
10,60 3871,56 1917,60 1917 Aug 5 AD 57.3 125.7 291.6 300 10
10,80 3944,63 1928,40 1928 May 24 AD 21.9 256.4 125.5 120 4
9,00 3287,18 1937,40 1937 May 24 AD 288.9 358.4 290.5 300 10
10,10 3688,94 1947,50 1947 Jun 30 AD 237.1 131.8 105.2 120 4
Furthermore, we will only list "factors" for the given periods. We omit transition periods. From the last 250 years (1750-2000) we receive:
Period Factors
----------------------
1738-1769 10,5,12,4
1816-1848 9,4, 9,4
1917-1947 10,4,10,4
1957-1989 10,5,11,5
Factor 9-11 corresponds to angles 270-330 degrees, factor 4-5 angles 120-150 degrees. Therefore, the maxima occur at 120 dg and 300 dg much more often than at 240 dg. Similar observations for minima give 30 dg and 210 dg.
Extremes occur in quadratures that are delayed - about time of the interval for which the J-S take 30 dg.
For a longer period of 0-2000 years of Schove's data, there are some shifts, but their origin could not be identified.
Collapse of the cycle phase
In previous statements, we missed 2 seasons - at about 90-100 years distance:
Interval Days Extreme of activity J S J-S Angle Factor
---------------------------------------------------------------------------
8,70 3177,63 1778,40 1778 May 23 AD 153.0 225.8 287.2 300 10
9,70 3542,83 1788,10 1788 Feb 3 AD 88.9 333.8 115.1 120 4
17,10 6245,63 1805,20 1805 Mar 12 AD 238.6 194.8 43.7 30 1
Interval Days Extreme of activity J S J-S Angle Factor
---------------------------------------------------------------------------
12,00 4382,91 1860,10 1860 Feb 3 AD 114.1 144.3 329.8 330 11
10,50 3835,04 1870,60 1870 Aug 5 AD 71.8 268.5 163.3 150 5
13,30 4857,74 1883,90 1883 Nov 22 AD 116.4 68.0 48.4 60 2
10,20 3725,45 1894,10 1894 Feb 3 AD 64.7 201.1 223.6 210 7
12,90 4711,63 1907,00 1906 Dec 29 AD 97.4 346.7 110.7 120 4
These are the so-called "collapses of the cycle phase" (loses of phase lock, phase catastrophes).
Transitional periods and quadratures
If all sun peaks are inclined to quadrature, (which appear on average with a 10-year period) the overall course would not match the observed (11-years) Wolf cycles. The shift occurs in transition periods.
In the next attempt, we place maxima of activity closest to quadratures. For example: Let's start with the maximum of 1705.5 and proceed to the next maxima with the Hale cycle about 22 years:
Quadratures 1707.7, 1727.4, 1748.2, 1767.3, 1786.9, ... ... 1817.1, 1837.0, 1856.9,...
Maxima 1705.5, 1727.5, 1750.3, 1769.7, 1788.1, ...(1796.0)... 1816.4, 1837.2, 1860.1,...
Cycles 1705-1727.5 belong to the first type of quadrature (Jupiter before Saturn), Cycles 1816-1860 are of the second type (Saturn before Jupiter). So between 1788 and 1816 something unusual happened - one half of the cycle has fallen out (see Gnevysev-Ohl rule). This is also associated with the possibility that the magnetic field of the Sun was polarized two times in succession around the year 1800,
We check that we have complied with the Hale's cycle during this shift:
(1856.94-1707.65)/7 = 21.35 years, (1860.1-1705.5)/7 =22.09 years.
Counterexamples of quadratures
In 1797, the quadrature of J#S was two years before the minimum of 1799, similarly 10 years later, the quadrature of J#S 1808 was preceded by a minimum of 1809. Three other examples are observed at about 100-year intervals:
Quadrature J#S Minimum
--------------------------
1767 1767
1868 1867
1966 1966
Quadrature J#S of the year 1857 adds to this, two years after the minimum 1855 - here also near the quadrature U#N (Uranus-Neptune)!?
Gleissberg cycle
When Q is the quadrature period (coinciding with the Hale peaks), W is the Wolf period and the magnitude of displacement between quadrature types is Q / 2, then the period P of shifts is:
P(W,Q) = k* Q + Q/2 = k * 2*W, from which k = (Q/2) / (2*W-Q).
For Q = 19.86 years and W = 11.05 years it results: k = 19.86/2/2.24 = 4.433, ie. k*2*W = 4.433 * 2 * 11.05 years = 2 * 48.98 years = c. 98 years. (Therefore k * Q = 4.433 * 19.86 = 88.04 years = cca 8 W = cca 98 years - 9.93 years).
The distance with which one type of quadrature passes in the other is about 98 years, which corresponds approximately to the period of the Gleissberg cycle, respectively. rather its possible higher limit.
The 90-100 year period was repeatedly derived by analyzing different sources. E.g:
Zdroj
----------------------------------------------------------
Abbot (Climate) (1937) 92 years
B.M.Rubasev (S-activity) (1964) 93 years
Wood (Lunar tidal cycle) 93 years
Feirbridge, Sanders (Lunar) 93.02 years
Libby (tree rings) (1983) 95 years
According to the relationships above, the quadrature modulation period could be longer. This would explain the observed mismatch with the Uranus-Neptune cycle ((U, N)/2 is about 85.5 years - see above Mörth-Schlamminger).
The observed 2P periods corresponds to the modulation periods
M = ((J,S), 2W), ie. 2P=M.
For Q = 19.86 years, we get the following values for selected lengths of the W cycle:
W k = (Q/2)/(2*W-Q) P=k*2*W M Source
----------------------------------------------------------
10.40 let 19.86/2/0.94 = 10.564 219.7 let 439.4 Okal and Anderson
10.81 let 19.86/2/1.76 = 5.642 122.0 let 244.0 Vukcevic
11.05 let 19.86/2/2.24 = 4.433 98.0 let 196.0 Schove
11.08 let 19.86/2/2.30 = 4.317 95.7 let 191.4 Wood
| Silvia Duhau , argentine researcher in the field of solar activity and climate change. She deals with the theory of the solar dynamo. |
S.Duhau and C.Y.Chen observed 2 periods of increase in solar cycle intensity (lasting about 35 years) near years 1705 and 1923. The interval of these periods is 218 years.
Lunar cycles of 8.85 years and 18.6 years are in the same phase every 186 years: 11 * (8.85, 18.6) = 186 years = 2 * 93 years (Louis M. Thompson, 1988).
Planetary positions on elliptical orbits
Transitional periods are given approximately by the years 1685, 1793, 1877. The last period (estimated to 2018?) seems to be delayed (compared to the estimated 90-100 years).
Note the following correlations of transition periods with approaching outer planets to their perihelions/aphelions:
Interval Year Date Index of proximity
219,00 1133,00 1132 Dec 22 AD 3.8039
250,00 1383,00 1382 Dec 20 AD 3.8236
165,00 1548,00 1547 Dec 19 AD 3.9081
250,00 1798,00 1797 Dec 28 AD 3.9677 ***
88,00 1886,00 1885 Dec 28 AD 3.9158 ***
161,00 2047,00 2046 Dec 28 AD 3.9366
88,00 2135,00 2134 Dec 29 AD 3.9026
Beats of cycles
Ernest W. Brown| Ernest William Brown, 1866-1938, English mathematician and astronomer living in America. Is known for his theory of moon movement. He dealt with the celestial mechanics, elaborated detailed lunar tables. |
Brown's period
Considering Jupiter's influences there is - according to E.W.Brown (1900) - necessary to add primarily influences of Saturn and then secondary influences of smaller bodies (noticing the 4-year periods in their mutual movement). He derive period (J, (J, S) / 2) = 61 years from Jupiter's and Saturn's movement.
Milivoj.A.Vukcevic| Milivoj.A.Vukcevic , [], theoretician of Serbian origin dealing with solar, geomagnetic and climatic phenomena. He defined solar envelope functions of solar activity. |
Vukcevic's relationships
Milivoj.A.Vukcevič presented in 2004 (in the "Evidence of a multi-resonant system within solar periodic activity") several remarkable relationships, which (within a defined time interval) cover the course of the solar cycle. One of his relationships is the sum of two cosine functions with arguments:
- A1(t) = (t-t01)/(J,S) = (t-t01)/19.859 let
- A2(t) = (t-t02)/2J = (t-t02)/23.724 let
The beats of these periods are approximately V1 = 120 years: ((J, S), 2J) = 122 years, Vukcevic states 118 years for the last centuries. (The asteroid Nessus moves with the same period in the solar system). In addition to this period, Vukcevic works with the period V2 = 288 years (287-290 years).
Note that the periods of these functions correspond to twice the period, of E.W.Brown: Brown's 61-year period vs. Vukcevic's 122 years. The first function presents spacing of Jupiter-Saturn, the second Jupiter advance on doubled(!) elliptical orbit.
The 61-year period can also be derived from long-term shifts of Jupiter-Saturn conjunctions, as they enter during the three-fold cycle (see Conjunctions).
Vukcevic's functions allow to explain lengthening of cycles in transition periods - the theoretical course of activity is nearly constant here. From this perspective, for example, adding another maximum for the year 1796 is superfluous.
For further context, see: Shape functions.
Valentina Zharkova| Valentina Zharkova , [], Ukrainian researcher in the field of solar physics acting as professor of mathematics and astronomy in England. |
Components according to Zharkova
Valentina Zharkova deduced - based on spectral magnetic analysis of the Sun field - two basic "principial" components. These components are very much like Vukcevic's functions. The difference between the two theories is in the prediction of the period of beats. Zharková points to a significant 350-400 year cycle (Z), which seems to be significantly different from Vukcevic's cycles.
Reflections on possible unification
The Vukcevic cycles (V1, V2) offer a connection with motion of Uranus (U) Neptune (N) and cycle of Zharková (Z). Let us quantify the beats (U, V1) and (N, V2): (U, V1) = (84.01, 120) = 280 years (=V2), (N, V2) = (164.79, 288) = 385 years.
So, approximately (U,V1) = V2 a (N,V2) = Z.
A similar concept is outlined in consideration about Planet X with period of X = Z. (see Planet X). Here are considered cycles X = 387 years (375-390 years) (N, X) = 287 years (= V2) and (U, X) = 107 years (= 3 * Bruckner = 9 * J). With regard to the Vukcevic concept, there is the course (N, X) compared to V2 phase shifted.
Note that for V1 = 118.6 years is (U,V1)= 288 years = V2. (10*J = 118.6 years, 6*(J,S) = 119.2 years).
Acknowledgment
I would like to thank in particular to RNDr.Pavel Kalenda CSc. for valuable information and resources that helped me to orientate in the field of the influence of planets on solar activity.