Conjunctions, inequalities
Introduction
We will use - from the three ways of expressing dates - mainly "the mathematical" and "the historical" way.
historical astronomical mathematical ------------------------------------------- 1.4.2005 AD 2005(.25) 2005.25 1.4. 1 AD 1(.25) 1.25 1.4. 1 BC 0(.25) 0.25 1.4. 2 BC -1(.25) -0.75 1.4.2005 BC -2004(.25) -2003.75
Synodic period
Periods of motion
Basic orbital periods of bodies are given with regard to stars. These are so called sidereal periods.
In the next computations we will use mean periods according to VSOP87 (Bretagnon, Variations Seculaires des Orbites Planetaires).
|
Outer planets |
Inner planets |
J 11.8620 years ( 4332.59 days) S 29.457159 years (10759.23 days) U 84.020473 years (30688.48 days) N 164.770132 years (60182.29 days) |
M 0.2408467 years ( 87.96926 days) V 0.6151973 years (224.70080 days) E 1.0000174 years (365.25636 days) R 1.8808480 years (686.97973 days) |
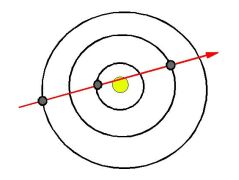
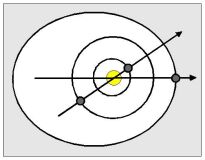
 Conjunction
Conjunction
Conjunction is a close apparition (join, alignment) of two or more bodies. For simplicity we will consider only alignment of bodies in plane perpendicular to approximate plane of planetary motion (i.e. conjunction in longitude). Exact alignments in one line are sporadic and they are studied in connection with other phenomena (eclipses of Sun and Moon, transits of Mercury and Venus through solar disc…)
If bodies are observed from the Sun, we speak about
heliocentric conjunction (conjunction with the Sun).
E.g. if bodies ordered Sun-Venus-Earth-Mars are in a straight line,
we say Venus-Earth, Earth-Mars, Venus-Mars and Venus-Earth-Mars are
in conjunction (seen from the Sun).
Practical astronomy understands by conjunction usually geocentric conjunction. If Sun-Venus-Earth-Mars are aligned, it is said, Venus is in conjunction and Mars in opposition (with the Sun, seen from the Earth).
Synodic period of two bodies
Mean period, with which (helio)centric conjunctions of two
bodies repeat, is called synodic period.
Synodic (relative) period of two periods P,Q is period:
(P,Q) = 1/(1/P-1/Q)= P∙Q/(Q-P)
We designate synodic period with round brackets ().
For any periods A,B and constant k it holds:
(A,B) = -(B,A) (k∙A,k∙B) = k∙(A,B) ((A,M),(B,M)) = (A,B).
In practical astronomy it is implied, that one of the period is
orbital period of the Earth. E.g. synodic period of Jupiter is
determined to be c. 399 days. It is period of Jupiter with regard
to Earth: (E,J) = (365.256,4332.59) = 398.9 days.
Se synodickou period se postupně rozvírá (a pak zase přivírá)
úhel P-S-Q; S is centrum, bod (center of gravity systems) okolo kterého
tělesa P,Q obíhají.
With synodic period the angle P-S-Q gradually opens (and then
closes); S is the point (centre), around which motion of bodies P,Q
happens.
|
Outer planets |
Inner planets |
(J,N)= 12.7822 years ( 4668.69 days) (J,U)= 13.8120 years ( 5044.81 days) (J,S)= 19.8589 years ( 7253.45 days) (S,N)= 35.8699 years (13101.47 days) (S,U)= 45.3602 years (16567.82 days) (U,N)=171.4443 years (62620.01 days) |
(M,R)= 0.276217 years (100.8882 days) (M,E)= 0.317255 years (115.8775 days) (M,V)= 0.395801 years (144.5662 days) (V,R)= 0.914227 years (333.9215 days) (V,E)= 1.598690 years (583.9214 days) (E,R)= 2.135349 years (779.9361 days) |
Synodic day
Synodic day is rotational period Tr measured with regard to orbital period T, i.e. synodic period (Tr,T).
In case of planet of the Sun we speak about “solar day”, e.g. if Earth as rotational period Tr =1 stellar (sidereal) day, is its solar day equal to (1.0, 365.256) = 1.0027 stellar days. We divide solar day to 24 hours.
Reversing of polarity
Let us have a number of small periods Pi: (P0, P1,..., Pn),
and greater period Q. If periods Pi have common multiple P, which
is approximately equal to Q, it could appear, all the system has
period P.
But evidently it is not true. Deviations of periods (P-Q) will
gradually accumulate; during synodic period (P,Q).
Such accumulation of deviations can appear as transformation of cycle P, as change of its polarity.
E.g. periods 3,4 and 13 years makes common multiple c. 12-13 years. It can be well approximated by period P=12 years. But after a longer time we will register beats with period c. (12,13)=156 years.
In solar system periods (U,N)= 171.44 years and 9∙(J,S)=178.730 differ by more than 7 years. Though they are usually covered by so called 180-years period. Deviations of periods oscilates with period c. (9∙(J,S),(U,N))=(178.7, 171.4)=4200 years.
I.Charvatova has found period c. 4400 years (resp. its aliquots 2200 years and 1100 years) in motion of the Solar system gravity centre. According to I.Charvatova is the basic interval made of c. 55 conjunctions (J,S), i.e. 1100 years. Observed deviations of motional characteristics are in turns positive and negative (intervals in years): (-2200,-1100) +; (-1100,0) -; (0,+1100) +; (+1100,+2200) -.
Cycle of great conjunctions- 4617 years: Santong Li; 243*19 years = 3*Thung; 65*71.03 years=65*65*1.0928 years
- 4627.1 years: similarity of patterns of J-S-U
- 4627.220 years: OP Res (Fairbridge,1997)
- 4627-4670 years: common period of all known planets (all planets synod)
Distortion
Mentioned definition of conjunctions is not physically correct, it is only geometrical construction. We neglect finite speed of light as well as time-space relations and so on.
E.g. to compare of conjunctions V-E (period 1.6 years) and conjunctions J-N (period 12.8 years), we have to consider space distance about 29 AU. (Light run this distance c. 4.3∙1012 m during c. 14300 seconds, i.e. c. 4 hours…).
Venus-Earth interaction
Four-years periodFour-years period was found in a number of biological and economic phenomena. It was used by ancient Greeks (the Olympics period) as well as by Mayan astronomers (cycle of 4 naming days). According to Wood, there is cycle of Moon tides of length 4.001 years.
- 7.993 years (2919.6 days): 5*(V,E)
- 7.995 years (2920 days): Mayan period
- 8 years: frequency of storms (Aniol, 1952)
- 8 years tropical = 5 synodical oběhů V + 2 days
- 8.000 years (2922.0 days): Venušin koincidenční cycle 5*(V,E)=2919.6097 days (starší měření); 2919.57 days (radarová měření)
- 8.0 years: Turkish cycle (5*354+3*355=2835 days); chyba 1d/(126*29.53)d
- 8.0 years: 5*(V,E)+2d=8 years; 8 years+2d=99 (E,L)
- 99*(E,L) = 99*29.53059 days = 2923.53 days =8.00418 years
-
5*(V,E) = 5*583.9214 = 2919.61 days = 7.99345 years.
(E.g. conjunctions V-E: 6.4.1977, 3.4.1985, 1.4.1993,...). - 8.004 years (2923.5 days): Lunar phases (99 lunations)
- 15.771227 years: (E,R/2); beat(E,R), 1:2
- 15.8087 years: 4/3 J
- 16 years: climatic cycle
- 16 years: Greek cycle; 29.53059*198=5847.057 d; 365.2422*16 =5843.875 d;
- 15-17 years: variation of distances E-R (Mars - Perihelion Opposition)
Internal cycle
By „internal cycle” we mean cycle of inner planets with period I=6.4 years.
Period I
Resonance 3:4:7 of synodical periods Venus, Earth and Mars:
- 6.394758 years: 4*(V,E) = 4*1.5986896 years.
- 6.399591 years: 7*(V,R) = 7*0.9142273 years.
- 6.406046 years: 3*(E,R) = 3*2.1353487 years.
- 6.391093 years: (J,N)/2 = 12.7821869 years /2.
- Mayan cycle 9 tzolkin: 9*z= 2340 days= 6.4 years, a combination of three main numbers 9 (lords of nights), 13 and 20.
- Stable resonance (J,S/3,-U,-N/3)= 2340.8 days =6.41 years.
Period 6.4 years
Indication of regularity
Conjunctions Venus-Earth-Mars repeats approximately every 6.4 years. During 4 conjunctions V-E, 3 conjunctions E-R appear.
This motion repeats regularly like clockwork.
V-E E-R
--------- --------
1886.140 1886.181
1887.728
1888.281
1889.335
1890.406
1890.929
V-E E-R
--------- --------
1892.528 1892.593
1894.132
1894.806
1895.720
1896.949
1897.330
V-E E-R
--------- --------
1898.923 1899.055
1900.520
1901.147
1902.127
1903.241
1903.715
V-E E-R --------- -------- 1905.322 1905.352 .... ....
If conjunctions could be heard, the sound would remind a drummer that play 3 triplets during 4 beats (beats are conjunctions Venus-Earth).
- 6.394758 y: 4*(V,E) = 4*1.5986896 years
- 6.399591 y: 7*(V,R) = 7*0.9142273 years
- 6.406046 y: 3*(E,R) = 3*2.1353487 years
(E,R)/(V,E)= 779.9361 days/583.9214 days= 2.1353487 years/1.5986896 years= 1.335687.
(E,R)/(V,E) ~ 4/3
Missing loop?
V-E E-R
----------- -----------
2039.6081 2040.0078
2041.2152
2042.1051
2042.8032
2044.1968
2044.4104
----------- -----------
2046.0066 2046.2968
2047.6000
2048.4269
2049.2099
2050.6200
2050.7979
----------- -----------
2052.4023 2052.8267
...
After c. 150 years regularity of conjunctions V-E-R quite disappear (see outline on the right):
Entire cycle repeats with period c. 300 years.
Ratio (E,R)/(V,E) is not 4/3 (192/144), but rather 191/143. After c. 300 years one conjunction V-E and one E-R "drops out": 191∙ 1.5986896 years = 305.350 years, 143∙ 2.1353487 years = 305.355 years
So: (E,R)/(V,E) = (4∙48-1)/(3∙48-1); 48∙((V,E),(E,R)) = 48∙ 6.361133 years = 305.334 years
Mayan evaluate period: 140*(E,R)= 140*780 days = 109200 days
(299 years=23*13 years), or 187*(V,E).
In this case: (E,R)/(V,E) = (4*47-1)/(3*47-1).
Likewise: (4∙(E,R))/((V,E),(E,R)) = (4∙12-1)/(3∙12-1) or R/Ey=(2∙54-1)/54=107/54, see Ecliptic year.
Line configurations
Instants, when configuration Earth-Venus-Mars makes a line, repeat also (like conjunctions) approximately with period 6.4 years. Besides, another structure appears here:
Mars stays four times (three periods R) at the same place.
Later (after 6.4 years from the beginning) the same pattern starts again
(phase shift F, c. 250-300 days).
Let: 3*R + F = 6.4 y. Then F = 6.4 - 3*1.880848 = 0.757 years = 276.7 days.

Date (Interval) Time ----------------------------------- 1885 Mar 29 (1.88364) 1885.24820 1887 Feb 9 (1.86721) 1887.11545 1889 Jan 3 (1.90007) 1889.01556 1889 Oct 1 (0.74196) 1889.75754 1891 Aug 23 (1.89185) 1891.64943 1893 Jul 8 (1.87543) 1893.52490 1895 Jun 5 (1.90828) 1895.43322 1896 Feb 10 (0.68446) 1896.11770 1897 Dec 29 (1.88364) 1898.00138 1899 Nov 17 (1.88364) 1899.88506 1901 Oct 9 (1.89185) 1901.77696 1902 Jul 31 (0.80767) 1902.58464 1904 Jun 18 (1.88364) 1904.46832 ...
Every c. 300 years one period R "vanishes". Complete cycle 6.4 y vanishes after c. 1020 y (300 y*6.4/1.88)?
Period 12.8 years
Mayan period 13 tun
Period 13*18*20 days = 4680 days (12.81 years).
13 Mayan tuns = Double period of conjunctions V-E-R:
- 8*(V,E) = 12.789516 years = 2* 6.394758 years
- 6*(E,R) = 12.812088 years = 2* 6.406044 years
- Mayan cycle 18 tzolkin: 18*z= 4680 days = 12.81 years
- ([J,N],U)= 12.74 years
- (J,N)= 4668.7 days= 12.78 years
- (U/2,S/3)= 12.81 years,...
- 12.74 years: ([J,N],U)
- 12.743 years: (2.2066,1.8809)
- 12.74682 years: ze simulation motion center of gravity známých planet
- 12.76 years: solar spectrum (Charvátová)
- 12.79100 years: simulation motion center of gravity známých planet
- 12.79891 years 14 conjunctions V-R (beats 9867.3 years)
- 12.8 years významná period ve Slunečním spektru (Charvátová)
- 12.81184 years: 18 tzolkin = 18*0.71177 years
- 12.81475 years: (2/U,3/S)
- 25.6237 years: 36 tzolkin = 36*0.71177 years
Mars in perihelion
Because frac(6.4/1.88)= 2/5, observer of Mars with period 6.4 years realizes, that Mars makes pentagon like as conjunctions V-E, frac(1.6/1.0) = 3/5. Oppositions V-E, Mars at perihelion:
Rozdíl Datum Lv Le Lr Lv-Le -------------------------------------------- ( 31.98) 1715.86: 47.6 228.2 326.0 -180.6 ( 31.98) 1747.84: 38.7 219.9 326.6 -181.1 ( 31.98) 1779.81: 29.9 211.5 327.2 -181.6 ( 31.98) 1811.79: 21.2 203.2 327.8 -182.0 ( 31.97) 1843.76: 12.1 194.2 328.2 -182.1 ( 31.98) 1875.74: 3.5 185.8 328.8 -182.3 ( 31.98) 1907.72: 354.9 177.4 329.4 177.5 ( 31.98) 1939.69: 346.3 168.9 330.0 177.4 ( 31.98) 1971.67: 337.8 160.5 330.6 177.3
Conjunctions V-E repeat their position relative to Earth every 8 years and conjunctions V-E-R occur with a period 6.4 years. Thus conjunction V-E-R occurs approximately at the same location relative to the Earth after 32 years: 32 years = 3∙10.67 years = 4∙8.00 years = 5∙6.40 years.
- 32.0 years: series interval between V-R repeated conjunction
- 32.03 years: 45 Tzolkin
- 32.0-33.9 years: V-R conjunction (R in perihelion) (avg:J*25/9)
View from Mars
Seen from Mars: Venus moves forwards with period (V,R/3)=32.819643 y, meanwhile Earth moves backwards with period (E,R/2)= 15.780949 y.
Resultant motion makes period: [32.819643, 15.780949] =
10.656765 years. Five periods (E,R): 5*(E,R) = 10.676744 years.
Equality of these periods gives unstable resonance:
5/V - 6/E - 4/R = 0 (1139 years)
Note: modulation (10.656765, 302.4347) = 11.046 years.
Other periods
Period 256 years
Mayan period. 13 Mayan katuns make 256.3 years.
Triple conjunctions J-S (observed from the Earth) returns after 257-258 years; e.g. 333, 411, 452, 710, 967, 1008, 1306, 1425 AD.
Incorporation of Mars
The eccentric orbit of Mars should be in accordance with the movement of Jupiter and movement of other internal planets.Resonance of beats
Integer ratios of pairs Mercury-Earth (E/M=4/1) and Venus-Mars (R/V=3/1) lead to beats
:- R1 = (E/4,M) = (1.0000/4, 0.2408) = 6.575 years,
- R2 = (R/3,V) = (1.8808/3, 0.6152) = 32.82 years,
1/M-5/V-4/E+15/R = 0
Expression Lx = Lm - 5*Lv - 4*Le + 15*Lr, where Lm, Lv, Le and Lr are longitudes of planet M,V,E and R,repeats its values approximately with orbital period of Mars.
Values of Lx
| Lx+45 | 1909,62 | 1922,79 | 1935,95 | 1949,12 | 1962,28 | 1975,45 | 1988,62 | 2001,78 | 2014,95 | |
| 0 | 0 | 29,2 | 353,3 | 0,3 | 16,6 | 333,2 | 347,2 | 26,8 | 341,0 | 352,3 |
| +1,88 | 0 | 2,5 | 353,7 | 23,6 | 359,9 | 336,7 | 4,0 | 359,2 | 341,0 | 17,6 |
| +3,76 | 0 | 330,4 | 9,7 | 26,4 | 342,5 | 0,9 | 8,1 | 330,3 | 355,1 | 23,1 |
| +5,64 | 0 | 339,0 | 23,4 | 351,4 | 355,7 | 23,3 | 341,5 | 337,9 | 7,6 | 350,2 |
| +7,52 | 0 | 3,4 | 14,4 | 331,3 | 15,4 | 20,7 | 334,0 | 0,9 | 0,0 | 330,9 |
| +9,40 | 0 | 25,3 | 340,1 | 341,3 | 27,2 | 345,4 | 354,9 | 20,2 | 327,1 | 341,7 |
| +11,28 | 0 | 17,9 | 338,5 | 2,1 | 7,1 | 335,4 | 18,4 | 10,4 | 327,3 | 2,3 |
gradually shifts by 360° * 2/7, so - it makes heptagon.
| 5*Lv-15*Lr | 1909,62 | 1922,79 | 1935,95 | 1949,12 | 1962,28 | 1975,45 | 1988,62 | 2001,78 | 2014,95 | |
| 0 | 0.00 | 345,9 | 341,3 | 347,9 | 351,3 | 347,9 | 357,7 | 353,0 | 358,0 | 1,3 |
| +1,88 | 102,86 | 89,2 | 85,1 | 92,1 | 93,2 | 92,1 | 100,5 | 95,2 | 102,9 | 103,5 |
| +3,76 | 205,71 | 193,0 | 187,8 | 196,7 | 194,9 | 196,0 | 203,0 | 198,3 | 207,5 | 205,2 |
| +5,64 | 308,57 | 295,3 | 289,7 | 300,5 | 296,5 | 300,7 | 305,7 | 301,6 | 311,1 | 307,0 |
| +7,52 | 51,42 | 37,3 | 34,5 | 43,9 | 39,1 | 45,5 | 47,5 | 45,2 | 54,2 | 49,4 |
| +9,40 | 154,28 | 138,7 | 138,8 | 147,1 | 140,3 | 149,8 | 149,0 | 149,3 | 157,2 | 151,8 |
| +11,28 | 257,14 | 240,8 | 242,1 | 249,5 | 244,6 | 253,9 | 250,9 | 253,8 | 259,3 | 254,6 |
Inequalities
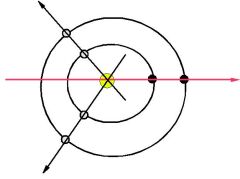
Period of inequality
Two bodies P and Q repeat their positions (e.g. in conjunction at the same place), if q periods P is equal to p periods Q, so if: q*P = p*Q, i.e. P/Q=p/q, where p,q are whole numbers.
Let
q/Q -p/P = 1/I
Period I is called period of inequality (or inequality period, inequality):
I = (Q/q,P/p) = P∙Q/(q∙P-p∙Q)
Usually I is on order of greater then P and Q (I>>P, I>>Q).
The place, where planets repeat their positions move with period I.
Big trigon
Conjunction of planets J and S appears on an average every
19.859 years. During this time Jupiter get approximately:
(J,S)/J *360° = 1.67416*360 = 360+242.698°. And Saturn
approximately (J,S)/S *360° = 0.67416*360 = 242.698°.
Because 240°=(2/3)*360°, conjunction places make equilateral
triangle, so called "big trigon". During 19.859 years this trigon
moves by
((J,S)/S - 2/3)*360° = 242.698-240 = 2.698°.
After 120°/2.698 * 19.859 y, i.e. c. 900 years (great inequality) the second apex appear at the starting point, and after c. 1800 years the third apex. The whole triangle returns to its original position after c. 2700 years.
If there was no rotation, conjunction line would be oriented
in the same direction every 3*(J,S). So, also after 42*(J,S),
45*(J,S) and 48*(J,S). During this period (c. 900 years) trigon
takes approximately 120° forward. Therefore conjunction line is
oriented in the same direction every c. 43, 46, and 49
conjunctions.
43∙(J,S) = 853.9 years, 46∙(J,S) = 913.5 years, 49∙(J,S) = 973.1 years
| Lambert, Johann Heinrich, 1728-1777 German physicist, mathematician and astronomer. Dealt with perspective, spherical trigonometry, cartography, photometry, reflection and dispersion of light, algebra. |
Change of planetary speed
J.H.Lambert has noted, that mean speed of Saturn increased compared to speed from Galileo’s measurements. This deviation was later make clear by Laplace with help of effect of small denominators.
Great inequalityValue of inequality Jupiter-Saturn (so called "great inequality", long-period inequality, Laplace's period, ...) is not known with a good precision. It is assumed, the period is "about 900 years" (840-960 years?).
From Bretagnon data (J=11.861983 years, S=29.457158) we have: I = (J/2,S/5) = -883.3 years.
|
S/1 |
S/2 |
S/3 |
S/4 |
S/5 |
S/6 |
S/7 |
S/8 |
|
|
J/1 |
19.859 |
60.947 |
57.013 |
19.422 |
11.705 |
8.376 |
6.522 |
5.340 |
|
J/2 |
7.426 |
9.929 |
14.978 |
30.474 |
883.27 |
28.507 |
14.487 |
9.711 |
|
J/3 |
4.567 |
5.405 |
6.620 |
8.538 |
12.024 |
20.316 |
65.464 |
53.556 |
|
J/4 |
3.298 |
3.713 |
4.249 |
4.965 |
5.971 |
7.489 |
10.042 |
15.237 |
|
J/5 |
2.580 |
2.828 |
3.128 |
3.500 |
3.972 |
4.591 |
5.438 |
6.670 |
|
J/6 |
2.119 |
2.284 |
2.475 |
2.703 |
2.976 |
3.310 |
3.729 |
4.269 |
According to Ptolemaio's values (J=11.862923, S=29.465040) is: I = (J/2,S/5) = -909.0 years.
Earth swings with a period P, c. 25500-26000 years. Therefore motion of planet appears to be distorted. Corresponding "distorted" periods are called tropical periods. Let P=25750 years. Then J' = (11.861983, 25750) = 11.85652 years and S' = (29.457158, 25750) = 29.42350 years.
During 19.859 years trigon move by ((J',S')/S' - 2/3)*360° = 242.976°-240° = 2.976°.
After 120°/2.976 * 19.859 y, i.e. c. 800 years (i.e. great inequality seen from the Earth) the second apex appear at the starting point, and after c. 1600 years the third apex. The whole triangle returns to its original position after c. 2400 years.
|
S/1 |
S/2 |
S/3 |
S/4 |
S/5 |
S/6 |
S/7 |
S/8 |
|
|
J/1 |
19.8589 |
61.0913 |
56.7618 |
19.3784 |
11.6836 |
8.3628 |
6.5120 |
5.3319 |
|
J/2 |
7.4241 |
9.9294 |
14.9870 |
30.5457 |
800.940 |
28.3809 |
14.4464 |
9.6892 |
|
J/3 |
4.5654 |
5.4039 |
6.6196 |
8.5412 |
12.0347 |
20.3638 |
66.1358 |
53.0054 |
|
J/4 |
3.2962 |
3.7120 |
4.2479 |
4.9647 |
5.9725 |
7.4935 |
10.0541 |
15.2728 |
|
J/5 |
2.5792 |
2.8270 |
3.1274 |
3.4994 |
3.9718 |
4.5916 |
5.4406 |
6.6748 |
|
J/6 |
2.1184 |
2.2827 |
2.4747 |
2.7019 |
2.9751 |
3.3098 |
3.7293 |
4.2706 |
Seen from the Earth tropical periods seem to be the only true and correct periods. But we should be careful while computing derived periods. A slight difference of tropical and sidereal period causes in our example a quite different results (2400 y vs. 2700 y, see above).
(Some values in the table, e.g. 3.4994, 14.9870, come out near to integer fraction of terrestrial year. Value (J/3,S/4)=8.5412 years is equal to ecliptic year Y).
Babylonian period
Babylonian period is distinct period of motion of inner planets. It makes approximately 427 years.
Introduction
Ray Tomes included Babylonian period into his schemes (see Theoretical Cycles Periods ):
427.0 213.5 106.8 53.38 26.69
142.3 71.17 35.59 17.79 8.897 4.448 2.224
1. 415-425 years
2. 305-314 years
3. 260-280 years, affects moisture
4. 177-227 years, almost all, very pronounced,
an intensity cycle, affects temperature
(median 202 years)
5. 154-157 years, a length cycle, 13 Jovian years
6. 143-148 years, a length cycle, 13 average cycles
7. 104-105 years, half of the 200-year cycle
8. 85- 90 years
9. 78- 79 years, the Gleissberg cycle
10. 63- 67 years, 1834-1901, (1954-?)
11. 57- 59 years
12. 51- 52 years, 1783-1834, 1901-1954
13. 43- 45 years
E-Moon-R-J-S
It holds approximately: B/2 = 25*Y = 100*(E,R) = 225*(E,Ln) = 18*J, so
2*(E,R)/J = Y/2J = 9/25
Simulation of motion of R-J-S makes patterns with period 853.9 years.
Great inequality
Great inequality (J/2,S/5) makes c. 2*B=72*J=29*S=400*(E,R).
Let us assume I= 2∙B = 72∙J = 29∙S' = 43∙(J,S').
Then using J=11.8620 we get: I=854.06 years, B=427.03 years, S' =
29.450441 years. Synodic period (J,S') = 19.861925 years.
If value of great inequality J-S was just value I= 2*B=
854.06 years, then derived periods differ from the Bretagnon’s
periods by ratio:
S/S'=29.457158/29.450441 = 1.000228;
(J,S')/(J,S)=19.861925/19.8588709= 1.000154.
Overlapping of cycles
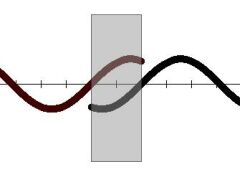
Separation of conjunctions
Synodic period is mean period of repetition of conjunctions. In reality conjunctions occur (in consequence of elliptical orbits and non-uniform motion of bodies) in irregular intervals.
E.g. conjunctions J-S, in years 1940-2000: 1940.85, (20.41), 1961.26, (20.01), 1981.28, (19.15) and 2000.43 (in parenthesis are intervals):.
Conjunctions J-S
Intervals of conjunctions Jupiter-Saturn repeats in triads, i.e. with mean period c. 60 years (Chinese astrological cycle), 3*(J,S) = 3*19.859 y = 59.577 y.
In every 900 years (great inequality) phase shift appears and new sequence of triads begins.
E.g. maximum separation c. 20.5 years appears before conjunctions in years 750.03, 1723.11 and 2636.65.
I. y. 750.03
0: ( 20.49) 750.03 ( 19.59) 769.62 ( 19.47) 789.08
1: ( 20.48) 809.56 ( 19.69) 829.25 ( 19.38) 848.63
2: ( 20.48) 869.11 ( 19.77) 888.88 ( 19.32) 908.20
3: ( 20.45) 928.65 ( 19.86) 948.51 ( 19.25) 967.76
4: ( 20.42) 988.18 ( 19.96) 1008.14 ( 19.19) 1027.34
5: ( 20.38) 1047.72 ( 20.04) 1067.76 ( 19.15) 1086.91
6: ( 20.34) 1107.26 ( 20.11) 1127.37 ( 19.14) 1146.50
7: ( 20.29) 1166.79 ( 20.18) 1186.97 ( 19.12) 1206.09
8: ( 20.22) 1226.31 ( 20.26) 1246.57 ( 19.12) 1265.70
9: ( 20.15) 1285.85 ( 20.31) 1306.16 ( 19.15) 1325.32
10: ( 20.07) 1345.39 ( 20.36) 1365.74 ( 19.19) 1384.93
11: ( 19.97) 1404.91 ( 20.41) 1425.32 ( 19.25) 1444.57
12: ( 19.88) 1464.44 ( 20.45) 1484.90 ( 19.30) 1504.20
13: ( 19.78) 1523.98 ( 20.48) 1544.46 ( 19.37) 1563.83
14: ( 19.70) 1583.53 ( 20.48) 1604.01 ( 19.47) 1623.47
15: ( 19.59) 1643.06 ( 20.49) 1663.56 ( 19.55) 1683.11
II. y. 1723.11
0: ( 19.51) 1702.61 ( 20.49) 1723.11 ( 19.64) 1742.75
1: ( 19.41) 1762.16 ( 20.49) 1782.66 ( 19.73) 1802.38
2: ( 19.34) 1821.73 ( 20.47) 1842.19 ( 19.84) 1862.03
3: ( 19.26) 1881.29 ( 20.44) 1901.73 ( 19.92) 1921.65
4: ( 19.21) 1940.85 ( 20.41) 1961.26 ( 20.01) 1981.28
5: ( 19.15) 2000.43 ( 20.37) 2020.80 ( 20.08) 2040.88
6: ( 19.14) 2060.02 ( 20.31) 2080.34 ( 20.16) 2100.50
7: ( 19.11) 2119.61 ( 20.25) 2139.86 ( 20.23) 2160.09
8: ( 19.12) 2179.22 ( 20.18) 2199.39 ( 20.30) 2219.70
9: ( 19.12) 2238.82 ( 20.11) 2258.93 ( 20.34) 2279.27
10: ( 19.16) 2298.44 ( 20.01) 2318.45 ( 20.40) 2338.85
11: ( 19.22) 2358.07 ( 19.92) 2377.99 ( 20.44) 2398.43
12: ( 19.27) 2417.70 ( 19.82) 2437.52 ( 20.47) 2457.99
13: ( 19.34) 2477.33 ( 19.73) 2497.06 ( 20.49) 2517.55
14: ( 19.43) 2536.98 ( 19.63) 2556.61 ( 20.49) 2577.10
III. y. 2636.65
0: ( 19.51) 2596.61 ( 19.53) 2616.15 ( 20.51) 2636.65
1: ( 19.60) 2656.26 ( 19.45) 2675.71 ( 20.49) 2696.20
....
| Spörer Gustav, 1822-1895, amateur astronomer, discovered independently from R.Ch.Carrington the time dependence of the occurrence of spots on the distance from the equator - 'Butterfly diagram' and expressed assumption that the Solar activity before y.1716 was very weak. |
Phase of new cycle is always shifted by on an average
(J,S)=19.859 y with regard to the previous cycle.
Phase shifts cause, that the mean cycle of conjunctions (with
regard to intervals of separation) seems to be (statistically,...)
little bit longer, approximately 19.859*(n+1)/n, where n is c.
42-48.
Triads then lasts c. 61 years, i.e. approximately (J,S/2)=60.95
years (1/7 of Babylonian period 427 years).
Long-term changes
Greatest deviations from mean intervals of conjunctions of planet Jupiter and Saturn are caused:
- by planets Jupiter and Saturn itself (elliptical orbits, great inequality)
- by planets Uranus and Neptune (perturbations).
-
Mean cycles of these changes are:
- cycle of 60-61 years (59.58 y, with phase shift, see above)
- cycle of 85.5 years (85.72 y = (U,N)/2 = 171.44/2 y)
Let us try to put these two cycles together.
With regard to phase shifts, we will write one function for
each interval (c. 800-1000 years).
The exact instants of shifts are not clear - perhaps they even
do not exist - one cycle fades while the other one become
stronger:
Interval Function
-----------------------------------------------------------------
(-2000,-1000) |Ap∙sin(2π(t-1111)/P)+Aq∙sin(2π(t-1157)/Q)|
(-1000, 0) |Ap∙sin(2π(t-1131)/P)+Aq∙sin(2π(t-1157)/Q)|
( 0, 1000) |Ap∙sin(2π(t-1151)/P)+Aq∙sin(2π(t-1157)/Q)|
( 1000, 2000) |Ap∙sin(2π(t-1171)/P)+Aq∙sin(2π(t-1157)/Q)|
( 2000, ... ) |Ap∙sin(2π(t-1191)/P)+Aq∙sin(2π(t-1157)/Q)|
....
Here P=3*(J,S)=59.58 y, Q=(U,N)/2=85.72 y, Ap,Aq are
constants and t is time [years]. Values 1111, 1131, 1151, 1171
AD follows c. 20 years phase shifts.
The value 1157 AD was selected 20 years after conjunction (U,N).
Egyptian minimum (-1300,-1200), Homér's minimum (-800,-700)
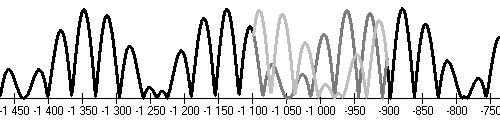
Greek minimum (-450,-350)
|
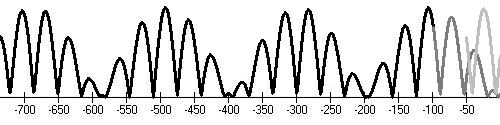
Middle age minimum (650,705)
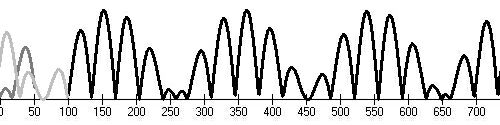
Middle age maximum (1120,1280), Wolf's minimum (1280,1340)
| Maunder, Edward Walter, 1851-1928 English astronomer, dealt with spectroscopy, photography of sunspot, observations of comets, Mars and the like. He confirmed the Spörer's assumption that Solar activity before y.1716 was very weak. |
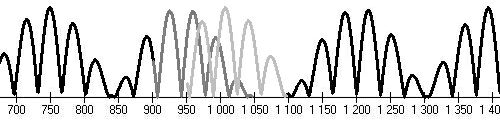
Sporer's minimum (1400,1500), Maunder's minimum (1645,1715), minimum (1870,1930), end of millenium maximum (1930-2030)
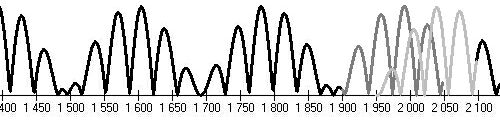
| Eddy, John A., 1931-2009, American astronomer, collected data from a variety of sources and reconstructed retrospectively values of solar activity. He specified period of so called Maunder's minimum (1645-1715) and defined so called Spörer's minimum (1460-1550). |
Comments:
Maunder's minimum started about 1650 AD. An analogous "zero-point" was e.g. at 800 AD, i.e. 850 years (2*B, i.e. 12 Bruckner's cycles) before Maunder's.
- Comparison with Schove's maxima:
- 175-200, (290-300?), 350-375, 500-510, 530, 565, 585, (675?), 745,765,
- (830-840?), 920-930, 960-980, (1100-1150), (1200), 1360-1370,
- 1530-1580, 1720-1740, 1770-1790, (1840-1870?), 1940-1990,...
- Diagrams fail to make clear minimum 1800-1820 AD.
- About 1820 conjunction J-S (1821.76), U-N (1821.01) (and barycentric loop) occured at the same time; J was in perihelion (1821.37).
- G.Sporer called attention to a possible low activity in years 1887-1889.
Other data:
| Minima | Maxima |
|
m2-1: 1040 m2-2: 1160 m2-3: 1270-1330 m2-4: 1410-1500 m2-5: 1670 m2-6: 1820 m2-7: 1880 |
M2-1: 1130 (1100-1150) M2-2: 1190 (1170-1220) M2-3: 1370 M2-4: 1610 M2-5: 1720-1780 M2-6: 1860 M2-7: 1960? |
Synchronization of deviations
Both mentioned cycles coincide with Babylonian period c. 427 years: 61.0 ∙7 = 427.0 years, 85.5 ∙5 = 427.5 years.
Derived periods
[(J,S/2), (U,N)/2]= [60.95, 85.72]= 35.6 years (Bruckner's period),
((J,S/2), (U,N)/2)= (60.95, 85.72)= 210.9 years (half of Babylonian period).
Are these cycles synchronized? Let us assume, it holds:
P=a1*P1+F1 = a2*P2+F2, where a1=14, P1=59.577 years, F1=19.859
years and a2=5, P2= 171.44 y, F2=?
Then P = 14*59.577 + 1*19.859 = 43*19.859 = 853.94 y
(2*B) and phase shift F2 = P- 5*171.44 = -3.27 y.
If F2= 0, then (U,N) = 2*B/5 = 2*36*J/5 = 427.031/5=170.813
y.
And hence Neptunian period: N = ((U,N),U)= (170.813, 84.020)=
165.358 y (deviation 0.4 % from Bretagnon mean period 164.770 y).
Prediction
For years 2000-2700 AD.
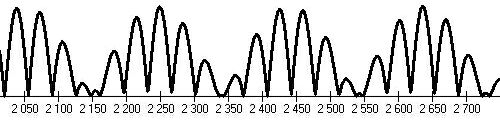
There would be next "Maunder's minima" around years 2150, 2350 and 2500?!.
Other relations
Conjunctions E-R
Conjunctions E-R appears close to geometrical axis J-S with period B/4. E.g. (with accuracy 5°) in years 1636.3,1743.2,1850.0 or 1869.1 and 1975.9.
It holds:
([J,S]/2, Y) = 2∙B
i.e. [J,S]/2, 4∙(E,R))= (16.9132418/2, 4∙2.1353487)= (8.45662, 8.54140)= 852.04 years= 2∙426.02 years.
Outer planets
Lt us assume two relations:
- synchronization of axes of outer planets with Jupiter
([J,U],[S,N]) = 3∙J
- synchronization of axes of outer planets with solar cycle
([J,N],[S,U]) = 4∙W
From equations (1/J+1/U)-(1/S+1/N) = 1/(3J) and (1/J+1/N)-(1/S+1/U) = 1/(4W) it follows W= 3/4(J/2,S/3)= 11.23375 years = [J,212.1 years].
And hence:
W= 3/4(J/2,S/3)= [J,B/2]
(But in comparison with the mean period of Solar cycle Ŵ=11.0-11.1 years is value 11.23 years too high).
Derived periods
Period 71 years
Babylonian counted also with the cycle B/6 = 6*J = 71.17 years (see Earthquakes).
65 oscillatory years give c. 71 years, i.e. 6 orbital period Jupitera.
1.091854 years: 9/2*(E,R/2)/65 = 9/2*(0.999979,1.880711/2)/65 = 70.97052/65 = 9/2*15.7712270/65
- 70 years: geological cycle (mud of Lake Saks)
- 70 years: cycle from tree rings (Japanese cedar tree)
- 70.9856 years: 65 oscillation years, 65*(E,J)=65*1.0920855 (tropical)
- 71.1391 years: 6*J (tropical), 71.1769 years: 6*J (anomalistic) =100 tzolkin
- 71.1785 years: B/6 = 427.07 years/6
- 71.1861 years: 4627.1/65 (925.4/13)
- 71.74 years: 2*(S,N) =2*35.87 years
- 73 years: geological cycle (banded clays)
Period B/2
Extrapolation of low solar activity from 1800-1830 to 1980-2010 went wrong, 180 years cycle failed. But in this case also 320 years cycle go wrong, because of Maunder’s minimum in years 1660-1690.
Schove, Derek Justin| Schove, Derek Justin , (1913-1986) English meteorologist and astronomer engaged in dating historical events in relation to natural phenomena (eclipses, auroras, floods, storms, etc.). Author of many papers, articles and books. Reconstructed retrospectively values of solar activity. |
In Schove’s dates periods of high (SSS,SS,S) and low (WW,W) solar activity seems to change with period more than 180 years. E.g. progress with step 205 years (about half of Babylonian period) we get e.g. years: 350, 555, 760, 965, 1170, 1375, 1580, 1785, 1990. Nearby (±40 years) of these dates relatively high maxima appear. (Tidal action of planet J-V-E cannot make such differences…!?)
Period 284 years
Simulation of motion of inner planets (with Bretagnon’s data) establishes especially part 2/3 of Babylonian period, i.e. period c. 284 years
Period 1025 years
I have noted the possibility of phase shifts of conjunction cycles while reading texts (paragraph about period 1020-1030 years) of climatologist Timo Niroma:
More notable extremes of solar activity seems to appear every c. 1025 years, i.e. 6*(U,N), 12B/5:
"The auroral data of G. L. Siscoe of the years 450-1700 (Rev. Geophysics and Space Physics 18, 1980) give another chance to try to calculate a value for the 1000-year cycle. The lowest superminimum (smoothed) between 450 and 1450 appeared from 620 to 680. It precedes the lowest superminimum of this millennium, the Maunder Minimum in 1640-1700 by 1020 years. The next superminimum after this pre-Maunder is in 780-800, which apparently corresponds to the superminimum in 1800-1820 both by duration and relative height with a 1020 year delay. The third superminimum in the Siscoe data is in 850-880 corresponding to the superminimum in 1880-1920 about 1030 years later. The Siscoe supermaxima in 740-770, 820-850, and 900-930 correspond to supermaxima beginning 1030, 1010, and 1050 years later, so that a supercycle of 1020-1030 years in average length is rather apparent." ( Timo Niroma, "Sunspots: Sunspot cycles and supercycles and their tentative causes")
Period G.L.Siscoe 1025 years: 5125/5;
minima v Eddyho diagramu Solar activity (-9625,-8600,-7575,-6550,-5525,-4500,-3475, -2450,-1425, -400, +625, 1650, 2675, 3700)
Conjunctions Uranus-Neptune
Data in the following table progress in the rough with Babylonian period 427 years. On the left are instants of conjunctions E-Ln-R and instants of Jupiter in perihelion.
E-Ln-R Jp U-N --------------------------------- -2021.55 -2022.63 -1594.48 -1595.57 * (-1605.74) -1167.41 -1168.50 -740.34 -741.44 * ( -745.20) -313.26 -314.37 113.81 112.69 * ( 111.19) 540.88 539.76 967.94 966.83 * ( 965.47) 1395.01 1393.90 1822.08 1820.97 * ( 1821.01) 2249.15 2248.04 2676.22 2675.11 * ...
Possible correlations with conjunctions Uranus-Neptune are marked on the right.
If mean period (U,N) was 170.813 years, then it would be equal to 20* Y= 80* (E,R)= 240 z. It would have integer ratio to Babylonian period (2:5), to 1025 years period of polar lights G.L.Siscoe (1:6) and also to Mayan period M=5125 years (1:30).
The following data (with period M/5 = 5125/5 = 1025 y)
seams to appear near to minima on Eddy diagram of solar
activity:
-9625,-8600,-7575,-6550,-5525,-4500,-3475, -2450,-1425, -400,
625, 1650, (2675), (3700).
These data (with period M/3 = 5125/3 = 1708 y) remind
great eruptions of volcanoes:
-5049 ?, -3341 Avelino, -1633 Thera, 75 Vesuvius, 1783 Laki, 3491 ?.
Laplace's cycle
Cycle of approximately 900-years (840-960 years?) created by the so-called great inequality of the planets Jupiter and Saturn. G. Beutler in the book Methods of Celestial Mechanics gives period 890 years, prof. A.E.Roy writes in the book Orbital motion about 900-year oscillation. Last extremes of Laplace's cycle was approximately in years 1560 (minimum) and 2000 (maximum).
Synchronization of perihelia
Mayan calendar round (52 years) and computation of tuns (1-18) makes period 9 Aztec centuries i.e. 9*104 = 936 years.
With the same period perihelia of Jupiter and Saturn synchronize. Value (Ja/2,Sa/5) computed from anomalistic period Ja,Sa makes c. 938-939 years.
Laplace's periodPeriod was observed in the following phenomena:
- 800-900 years: variation of returns of Halley comets (max spacing in years 450, 1250,.., min spacing in years 900,1800,...)
- 800-900 years: cycle of little ice ages
- 850-950 years: cycle of solar activity
- 850 years: in spectrum of solar motional characteristics (Charvátová)
- 853.9 years: R-J-S similar patterns 854 years: advance and regression of icebergs (Winkless, Browning)
- 882.62 years: 25/9 * 317.74 years = 16*25/9 * 19.8589 years
- 883.06 years: Laplace’s period (J/2,S/5) (sidereal)
- 893.66925 years: 417.0456+476.6236 = 45SJ/Ecc (Fairbridge,1997)
- 916.4 years: 15*61.09 years
- 925 years: cycle of ice ages (1850/2) (5*185 years)
- 936 years: Mayan cycle, 9 Aztec centuries
- 938.1 years: (J/2,S/5) (anomalistic)
- 939 years: J-S synchronization of perihelia
- 953.2472: 48SJ/US (Fairbridge,1997)
Mean Day Motion
The values nP=360/P are generally called the Mean
Angular Velocities (MAV), see
Angular
velocity.
If period P is given in days, we speake about
Mean Day Motion (MDM).
If in given time planet run just with mean velocity, its
motion is sometimes called "true motion" (=mean motion).
If a planet is in state of true (mean) motion, its actual
period is the mean period.
Actual velocity of motion deviates from velocity of
true (mean) motion.
Precision
Precision of antique astronomical
instruments was not better than c. 10’ (0.167 dg)
- in comparison with that precision of
values in age of Edmund Halley achieved 10”.
However the precision of some results in antique was very high,
e.g. Hipparchos determined MDM of the Earth with the
precision 0.0435” (0.000012 dg). Values of MDM
given in the Almagest (by Claudius Ptolemaios) lead
- after correction of precession - to the following MDM
for Jupiter and Saturn: nJ=299,104581“ nS=120,422528“.
These values corresponds to periods
J=3600/299,104581 * 360/365,25 = 11.862923 years and
S=3600/120,422528 * 360/365,25 = 29.465040
years.
Bretagnon theory (VSOP) makes these MDM values: <nJ>=299.1283“ and
<nS>=120.4547“, i.e.
periods
:
J=11.861983 years, S=29.457159 years.
For year 2000 NASA provides these actual MDM
values: nJ=299.1124“ and nS=120.4943“.
The period (I) of the Jupiter –Saturn inequality period gets from ratio S:J near to resonance 5:2: I(J,S) = 1/(5/S-2/J) . Because the denominator is small, the resulting value strongly depends on precision of mean orbital periods of Jupiter and Saturn. From Bretagnon data I(11.861983, 29.457158) = 883.3 years, from Ptolemaio’s data I(11.862923, 29.465040) = 909.0 years.
Bretagnon values
Mean motion of Jupiter is in Bretagnon VSOP82 theory
defined by this row: LM = { 0.5995465, 52.969096500,-15e-7,
0.0}.
Here the value 52.9690965 determine change of mean longitude for
century in radians:
Then J = 360 * 100 / (52.9690965 * 180/PI) =
36000/3034.905674=11.8619832 years.
Value -15e-7 is a second order term (longterm change).
Perturbations are computed separately.
In theory VSOP87 is for the same (including perturbations) 915
terms, that have to be computed and summarized for one position of
Jupiter. Here are the first 3 terms, where starting row with
longitude 0.599546 corresponds to the value LM above.
In the second row is the great inequality term, the third row
belongs to resonance S/J = 2/1:
J S A B C
1/ 0 0 0.59954649739 0.00000000000 0.00000000000
2/ 2 -5 0.00573506125 1.44396306420 7.11354700080
3/ 1 -2 0.00062308554 3.41857056095 103.09277421860
Then other rows follow.
The 17-th row represents the mean motion of Jupiter, where the value 529.69096509460
(in radians for millennium) is.
J S A B C
17/ 1 0 0.00001824700 5.72883078185 529.69096509460
From this we get mean period of Jupiter:
J= 360 * 1000 / (529.69096509460 * 180/PI) =
36000/3034.905674=11.8619831585 years.
Then yet about 900 other terms follows. The values A, B
and C in row are substituted to the formula v= A* Cos(B+ C*t)
and summarized, so values with small A does not influence result
too much.
So, periods can be computed from the values C in rows according to
relation:
T = 2000PI/ C = 6283.1853/ C.
For the great inequality we so get: 6283.1853/7.113547 = 883.27
years.
For the resonance S/J = 2/1 is 6283.1853/103.09277 = 60.9469
years
(note, it is the Chinese 60-years period modulated by complete
cycle of the trigon of conjunctions J-S:
1/60.9469 = 1/59.579 – 1/2649.1).
English astronomer
Jeremiah Horrocks (1619 – 1641) found (in the year 1637)
random departures in mean motion of Jupiter and Saturn.
Edmunt Halley (1656-1742) noted
that MAV of the Jupiter (Saturn) increased (decreased) compared to
antique values. The theory of planetary
motion based on Newton laws then resulted into formula of
continual change:
nJ = 299.1283611” – 0.000 000 089 81” T, nS = 120.4546453” + 0.000
002 836” T ,
where T is time measured in Julian centuries (36525 days) from 0
January 1850 (the antique values for T=-20).
Further Edmund Halley clarified value for Saturn to
nS=120.4054”, confirmed that MDM of Saturn (in comparison with
antique) decreased and concluded that this change is due to mutual
gravitational perturbations of Jupiter and Saturn.
Johann Lambert (1728-1777) realized, that MDM of Saturn increased
compared to Halley value by 0,02” (Saturn accelerated) -
and from this started to be clear, that the observed phenomenon is
not continual change, but harmonic wave.
According to observations of the 18. century, there was
nJ=299,128361“, nS=120,454645“ and so 2nJ-5nS=-4,016503”
(=-0,0000194725 rad).
Pierre-Simon Laplace derived the long-term harmonic function
(with value 2nJ-5nS in denominator)
and computed, that theoretical results (that not include this
function) can differ from real planetary positions by 20’ (0.33 dg)
for Jupiter and by 50’ (nearly 1 dg) for Saturn.
Let us assume, that both Jupiter and Saturn was in the state of
their true (mean) motion at the year <t> = 1780 and that
they influence each other with Laplace period I = 4*220 = 880
years. Bretagnon''s values of mean motion
are <nJ>=299.1283“, <nS>=120.4547“.
We can assign these values of MDM to all the years:
-3500,-2620,-1740,-860,20,900,1780,2660,…
and also to theirs centers:
-3060,-2180,-1300,-420,460,1340,2220,…
The year 2000 is 220 years after 1780 and for
this date we have NASA values
(nJ=299.1124“, nS=120.4943“).
We can expect the same values also in
years: -3280,-2400,-1520,-640,240,1120,2000,2880,…
Let as
define functions:
Q = sin[ (t - <t>) *
2PI / I ],
nJ = <nJ> -
<aJ> * Q,
nS = <nS> +
<aS> * Q
and evaluate amplitudes from the above adjusted
values (for 2000 and 1780):
<aJ> = 299.1283“-
299.1124“ =0.0159“ and <aS> = 120.4943“-
120.4547“ =0.0396“.
Now we substitute all the known values:
Q = sin[ (t - 1780) * 2PI / 880 ],
nJ = 299.1283“ - 0.0159“ * Q,
nS = 120.4547“ +
0.0396“ * Q
For years 1340, 1560, 1780 and 2000 we get these MDM values and actual (osculating) periods.
| Year | Q | nJ | nS | Years | J | S |
| 1340 | 0 | 299.1283“ | 120.4547“ | -3060,-2180,-1300,-420,460,1340,2220 | 11.8620 y | 29.4572 y |
| 1560 | -1 | 299.1442“ | 120.4151“ | -2840,-1960,-1080,-200,680,1560,2440 | 11.8614 y | 29.4669 y |
| 1780 | 0 | 299.1283“ | 120.4547“ | -2620,-1740,-860,20,900,1780,2660 | 11.8620 y | 29.4572 y |
| 2000 | 1 | 299.1124“ | 120.4943“ | -2400,-1520,-640,240,1120,2000,2880 | 11.8626 y | 29.4475 y |
If amplitudes <aJ>=0.0159“ and <aS>=0.0396“ are changes of MDM, then after a year they reach about: <AJ>=0.0159“ * 365.25 =5.81“ and <AS>=0.0396“ * 365.25 = 14.46“
Maximum departure from a mean value appeara c. after 220
years:
<AJ,max>= 5.81“*220 =1278“ and <AS,max>=
14.46“*220=3181“
These values corresponds to 1278“/60=21.3‘ for Jupiter and
3181“/60=53.0‘ for Saturn.
M.Somerville evaluate it to be 19.78‘ and 48.04‘,
Paul Schlyter gets 19.92‘ and 48.72‘.
Energy
Some scientists consider about connection of Laplace's cycle
with observed millennial cycle of solar activity.
When Jupiter get - for its own accerelation - some
extra energy from the Sun, then some lost of the solar
energy would be observed. Years in which Q take the values
-1:
-9000,-8120,-7240,-6360,-5480,-4600,-3720,-2840,-1960,-1080,-200,680,1560, 2440,…
The year 1560 corresponds to so called Suess' minimum.
There was oposition of Uranus against other outer planets in years 691 and 1561 (difference 870 years):
Solar rotation
Synodical rotation period of the Sun seen from the Earth
was estimated to be c.27.275 days.
In some years before (~Maunder minimum) it was lower:
| 1611-13 | 26,163 days |
| 1625-26 | 24,913 days |
| 1642-44 | 24,300 days |