Solar activity - Cycles

You're reading an English translation of the original Czech page.

The main solar activity cycles are Wolf's 11-years and Hale's 22-years cycle
The last maxima of Wolf's cycle were in years 1979, 1989 and 2000 (List_of_solar_cycles).

Observation of sunspots

Schwabe, Heinrich Samuel

Schwabe, Heinrich Samuel 1789-1875, amateur astronomer and botanist. Since 1826, he started (in an effort to find intra-merkurial planet Vulcan) the detailed observations of the Sun. After years of observation in y.1843 he noticed a significant ten-year period of the occurrence of sunspots.

Schwabe's period

Period of ten-years

9.823563 years: S/3 (anomalistic)
9.85 years: temperature cycle (New Haven)
9.885526 years: Ja/P (Fairbridge,1997) , 9.9 years: cycle in various phenomena
9.93-9.94 years: cycle of solar flares, length of solar cycle (Charvátová)
10 years: Schwabe’s approximation of solar cycle, atmosphere, rotation E (also variation of field)
10.1466 years:9*1.1274 years, E-Moon
10.2 years: winter temperature cycle (Hudson Valley)
10.2-11.0 years: geomagnetic activity, 10.2-11.2 years: flare activity
10.0-10.3 years: one of period of triad (Charvátová)
10.24 years = 4*2.56 years, bimodal solar cycles 10 and 12 years
10.4 years: strong annual temperature cycle (Hudson Valley), cycle in tree rings (giant sequoia)
10.40 years: 52 years/5, 10.4163 years: B/41, 10.47 years: cycle of solar flares
10.54 years: ((J,S)/2,(U,N)), 10.566 years: ((J,S)/2,N)
10.8 years: volcanic activity, 10.80774 years: 3/J-2/S=5.40387 years, 10.81254 years: Jakubowski
10.00 years: Wilson 1. mode (116-124 months)

Wolf, Rudolf

Wolf, Rudolf, 1816-1893, Swiss astronomer, organizer of the first international project for tracking sunspots. Reconstructed solar activity back to y.1730 and adjusted mean sunspot period to about 11 years.

Wolf‘s period

10.7-11.5: changes in high of zone of flares (Gleissberg)
10.914 years: tritos = inex-saros (solar eclipses); 135 lunation (3987 days)
10.97 years: 32.9 years/3, 11 years: inversion of solar mg.field, 10 oscillation years
11.01: 2*5.504 years (M-V interactions)
11.03-11.14 years (Schove 1955, for period c. 500 years)
11.0324 years: 31/2 tzolkin = 15.5*0.71177 years, 11.03295 years: (J,S) * 5/9; 11.03942 years: 9/J-25/S
11.04 years: Barnes,1980(±2.02 years)
11.05-11.09 – mean cycle solar activity (Jakubowski), 11.0515 years: S*3/8; [18.62,27.19]
11.065 years: [J,5*32.9 years] = [J,164.5], 11.0657 years: [J,N] sidereal, maxima (Schove, through 2000 years)
11.08 years: acceleration and impulses of planets (R.Wolf), 11.0857 years: minima (Schove 1955, derived from 1932-155.2*n)
11.095080 years: [3J,2S] = 9*1.2328 years =177.52/16, 11.09551 years: [J,(U,N)] anomalistic
11.1 years: generally (Schwabe-Wolf’s, Astronomy 1947), between maxima (Ellison 1958)
11.1188 years = 3/S-1/U = 1/(S,U)+2/S = 1/(S,U)+2/U, 1/11.1188-1/11.0657 => H (2318 years)
11.121217 years: SSC, Sun-Spot-Cycle (Fairbridge,1997), 11.13: mean length (Mirošničenko)
11.1426 years: (V/2, E'/3) = (0.61518/2, 0.94899/3)
11.1719 years: nodal cycle of moon Dione, 11.17 years: 178.73/16 = 279.3/25
11.19 years: solar activity minima, 11.20 years: Mirošničenko 1986; 7*(V,E)
11.2 years: solar activity (4.2 vzestup+7 sestup), <11.2 years: (A.Rima 1961)
11.214 years: 4096 days =64*64 days (Chinnese cycle, see 384 days), 11.22788 years: 3/4*14.9705 years
11.233 years: ((J,S)/2, 170.8 years/2), 11.23845 years: (J,B/2) (anomalistic)
11.261 years: ((J,S)/2,U), 11.274 years:10*1.1274 years, E-Moon, 11.30 years: Dvořák, 1989
11.34 years: (2071 days) libration of Galilean moons (Meeus)
11.3480 years: 16*Tzolkin = 8*1.4185 years, 11.3883 years: [J,24 J] = 16 tzolkin = 12*346.6314 d
11.4 years: cycle solar flares (Winkless, Browning), sediments (R.J.Hugget), alignment Moon-Saturn; [18.61 years,29.46 years]
11.42 years: (M/3,(Moon,E))= (87.969/3, 29.530588)= 4171.4 d
11.5 years: analysis of wood from Ancient Greek c.(-600,-400)
11.67 years: Wilson 2. mode (135-145 months)

Half of Wolf’s period

Also referred to as a 5-6 year Hellmann's period.

5.125 years: temperature cycle (New Haven)
5.2 years: cycles in history (N.S.Nesterov) (R.Tomes) , 5.25 years: climatic cycle (de Boer, 1938)
5.504 years: 1/M-4/V+2/E+1/R (synchron. period h of inner planets)
5.5 years: atmosphere, rotation E (also variation of poles)
5.560608 years: JEV (Fairbridge,1997)
5.6 years: climatic cycle (Polli, 1950) , 5.6370 years:5*1.1274 years, E-Moon
5.7 years: cycle in Cotton Acreage

Hale, George Ellery

Hale, George Ellery, 1868-1938, American astronomer. He derived - based on observations of magnetic fields on the Sun - 22-year cycle.

Hale‘s period

22 years: solar flares, reversing of solar magnetismus, tree rings
22.065 years: 31 tzolkin = 31*0.71177 years,
22.18 years: ((J,S),189.8 years) (tropically)
22.40 years (67.2 years) 14 * (E,V) = Ts = 14*1.6 years
22.422 years: Dicke,1979 (±0.036 years),
22.4558 years: 3/2*14.9705 years
22.462 years: ((U,N),(J,S)), axes [S,U][J,N] right-angle (90˚) axes [J,S][U,N] angle 120˚
22.5 years: cycle of flood levels
22.56 years: N with regard to (J,S),
22.58 years: ((J,S),N), 22.6002 years
22.75 years: solar cycle (Winkless, Browning)
22.7766 years: 32 tzolkin = 32*0.71177 years
23.0 years: Hale’s solar cycle, cycle in tree rings (Abbot)
23.2 years: seismicity (+-6.4), 23.4 years: volcanism (+-6.0), 23.6 years: temperature

Abbot's period

44.45 years: [61.01,N]
44.77 years: V-E-J simulation, 4*11.19 years
45 years: double Hale's solar magnetic cycle
45 years: solar cycle (Precambrium)
45.2 years: cycle of flood levels
45.5532 years: 64 tzolkin = 64*0.71177 years
46 years: climatic cycle, cycle of growth rings of trees (Abbot, 1937)
46 years: transit of Mercury through Solar disc, 46=(6+7)+33=13+33 years
46 years: occultations of stars by the eclipsed Moon (65-19 years)

Gleissberg cycle

Cycle of solar activity, usually given to be 80-90-years (70-100 years) ( Solar_variation),
discovered by Wolfgang Gleißberg during research of the solar activity.
Gleissberg observed 17 cycles from the year 290 AD (with mean duration c. 78 years), see below.
Length of the cycle is not constant - it varies quite considerably (approximately 85 ± 15 years).
Chandler's period

40.0 years: changes Chandler (S-Moon-E)
40 years: [60, 120]
40 years: intensity of geomg. field, archeomg. intensity
40.50 years: beats 779.94/365.256 = 15/7 (1.004);
40.66 years: conjunction M-V-E patterns
40.67 years: 2*B/21 (anomalitic)
40.7 years: spectrum of solar activity (Vztahy S-Zeme III)
40.79 years: beats 686.96/365.256 = 15/8 (1.003)
40.82 years: beats ((M,V),(V,E)) (1:4)
40.84 years: beats [E,V]/[E,M]=583.921/115.877=5.0391
40.85 years: beat(4/E-5/V+1/M) = 5*8.169 years
40.88 years: (E/8,R/15) tropical
42.12 years: beats from J/V = 19.282

Gleissberg's period

77 years: floods on Nile (Hameed, 1984)
78 years: isotopes of oxygen (Grónsko) (Dansgaard, 1973)
78.5 years: cycle of growth rings of trees (a giant sequoia)
78.8 years: solar activity (Gleissberg)
79 years: solar cycle (Precambrium)
80 years: growth rings of trees v Californii (Maksimov, 1952)
80 years: level of Kaspic sea (Maksimov, 1952)
80 years: surovost zim (Evropa) (Maksimov, 1952)
80 years: Island - concentration of ice (Maksimov, 1952)
80 years: interdiurnal thermal (Berkes, 1955)
80 years: cycle of growth rings of trees (14C)
80.427 years: (J/2,6.4 years)
83 years: solar activity (Wolf, 1853)
83 years: growth rings of trees (sequoia growth per decade, Clough, 1933)
83 years: low levels of Nile (Clough, 1933)
83 years: crudeness of winters (Europe) (Clough, 1933)
83.034 years: 7*J
83.4 years: Gleisberg cycle (Fairbridge,1997)
84 years: Beijing rainfall (Burroughs, 1992)
86.124 years: 121 tzolkin = 121*0.71177 years
88 years: cycle of growth rings of trees (Japanese cedar tree)
88 years: aurora, 89 years: climatic cycle
83 years: E-J synodic multiple, 76*(E,J)
83.0397 years: 7*J
84.0 years: solar activity (Maximov)
88 years: aurora (north lights, polar flares)
89 years: Budapešť, Prague - klima (Thraen, 1949)
90 years: growth rings of trees (Moseley, 1940; Lamb, 1972)
90 years: drought (Moseley, 1944; Burroughs, 1992)
90.4 years: cycle of flood levels
92 years: cycle of growth rings of trees (Abbot)

Timing

The last maxima of Gleissberg cycle appeared approximately in years:
1710-1720, 1760-1770, 1840-1850 and 1950-1960..
The last minima of Gleissberg cycle then fit approximately to years:
1740, 1810, 1900.

Pull of Saturn, Uranus and Neptune

Configurations S-UN and SUN follows each other with period c. 18-21 years. So the interval of two configurations SUN is 2 times longer, i.e. approximately 40 years (e.g.1672 minus 1630 or 1851 minus 1810).
Now, years us consider configurations (not necessarily exactly aligned), in which the planets S,U and N “pull against” Jupiter (like three men with ropes) from the opposite site of the Sun.
Allowing wider angles (max c.60 dg from the exact oppositions on both sides) the set of configurations J-SUN extends to (years): 1630-1670-(1711),(1770)-1810-1850, 1950-1990-2030.

Gleissberg extremes

The first 2 triads (1630-1711, 1770-1850) corresponds to Gleissberg extremes:

1631 (1.10.1631)

1670 (1.4.1671)

1711 (1.6.1711)

1770 (1.1.1771)

1810 (1.11.1810)

1850 (1.8.1850)

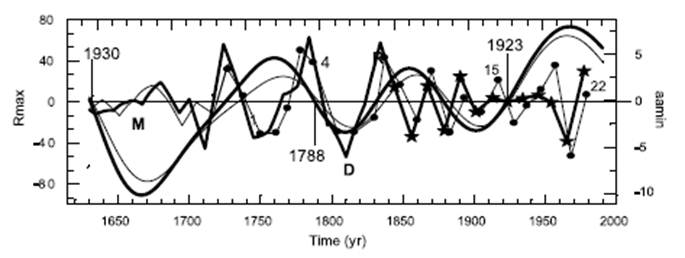
The year 1711

We mark (by red) the year 1711 as maximum here, because it ends the Maunder minimum.
But it is sometimes considered to be minimum.
So, probably, it is passing point - see the graph from the work of Prof.Silvia Duhau:

gleissberg01

Symetrical configuration

In some cases are "the ropes" of planets Uranus and Neptune nearly perpendicular to "ropes" of Jupiter and Saturn. E.g around the minimum 1890-1910:

1890 (1.1.1890)

1910 (1.1.1910)

Here are written some 100-year intervals, where no configuration J-SUN or only some weak configrations can be found: 660-760, 840-940, 1020-1120, 1160-1270, 1350-1450, 1530-1630, 1670-1770, 1850-1950.

Dificulty of prediction

Special alignment of the year 1990 reminds the year 1810, i.e. Gleissberg minimum.
But was the activity of the 1990 really longterm minimum? Do we have to expect maximum around the year 2030?

1950 (1.7.1950)

1990 (1.3.1990)

2030 (1.12.2029)

History

These intervals follows from the previous schemes:
580-620-660, 760-800-840, 940-980-1020, 1120-1160, 1270-1310-1350, 1450-1490-1530, (look on the Gleissberg cycles and some 180-year cycles...)

Gleissberg's extremes

Gleissberg (1965)

Gleissberg	U#N	J - SUN
?	64	84
?	150	124
?	236	263
360	322	303
440	409	443
510	495	483
575	581	583
665	667	662
755	754	762
840	839	801
920	926	941
990	1011	980
1115	1098	1120
1185	1183	1174
1250	1270	1299
1305	1270	1299
1375	1355	1353
1455	1441	1453
1545	1527	1491
1605	1613	1632
1715	1698	1671
1765	1784	1771
1840	1869	1851
1955	1955	1950
?	2041	2029

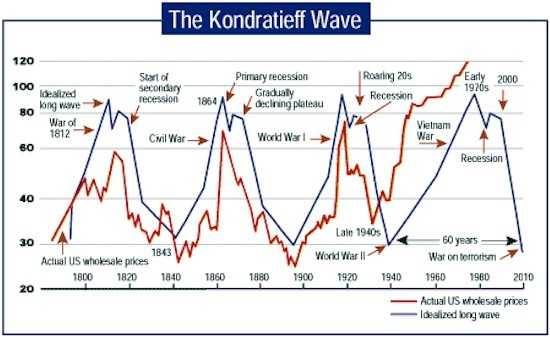
Kondratiev's cycle

Cycle of about 50-60 years, usually cited as of 54-year, see Kondratieff cycles , Kondratiev wave . The cycle was observed by Russian economist Kondratiev (Nikolai Kondratiev 1892-1938) and further studied by the American economist Dewey (Edward R.Dewey, 1895-1978).
It maybe linked with the 55-year cycle of solar activity.
The last extremes of the Kondratiev cycle were approximately in the years:
1810,1865,1920,1975 (maximum), 1835,1890,1945,2000 (minimum).
Cycle 55 years

The period was observed in the following phenomena:

53.0 +- 0.6 years - dominant periods of sunspots of years 1700-2010 (J.-E.Solheim)
53.2 years: cycle from tree-rings (a giant sequoia)
53.3 years: 5*10.66 years (J.-E.Solheim)
53.38 years: 9*J/2; B/8; 75 tzolkin
53.5558 years: 8/S-3/J, beats (J/3,S/8) - approximately 268 years/5 = 53.6 years
53.9 years: from spectrum of solar activity (textbook)
54 years: Contradieff economic cycle
54.093 years: Exeligmos=3*Saros, cycle of solar eclipses =669 lunations =19756 days
54.91 years: from spectrum of solar activity
55 years: cycle from tree-rings (Japanese cedar tree)
55.24 years: conjunction Jupiter-Uran, 4*(J,U)
55.33 years: M-V 224.701/87.969 = 2.5543 23/9 beats
55.408 years: [U,N] (tropical periods), 55.6449 years: [U,N] (sidereal periods)
56.1 years: cycle of solar spots
56.64 years: 1/J-3/S+3/U-3/N

Martin Roy on Solar Activity

Opposition Jupiter-Uranus

Mean period of 4 conjunctions J-U is 4*(J,U)=4*13.81=55.24 years:

Minima

29.4.1893 27.7.1948 31.10.2003

Maxima

16.12.1920 14.3.1976 12.6.2031

(http://dollarcollapse.com/wp-content/uploads/2010/05/Kondratieff.jpg)

110-year period and its multiples

Cycle 110.5 years

Minimum period 10 W ~ 110.3-110.6 years (i.e. c.10 W) appears in repetition of oppositions VEJ against U (e.g. about 1727.87, 1838.17 or 2058.78). Divisor of this period is also – excepting (J,U) - period 10.05 years of conjunctions (V,R),(R,S) and (V,S) (in relation to solar maximum y.1727.1).

110.31: V-E-J simulation 2*44.77+20.77 years, 10 * 11.031 years
110.500 years: 8*(J,U) = 8*13.8125 (317.77/3 = 105.923 years)
111.050 years: Moon tides cycle (Wood)
112 years: 4*28 years, "calendars of weather", "centennial calendars"

Wood‘s resonance

Year	∆L_JU	L_W[˚]
643.85	3	9
753.59	-4	10
863.92	-1	9
974.97	-5	-7
1085.42	-9	2
1195.35	-9	-2
1306.56	0	-8
1416.79	-5	-9
1527.02	4	-9
1637.71	-5	-9

Let L_w = 3*L_V-5*L_E+2*L_J [˚] . Period of Wood’s resonance (see Solar activity) makes 11.06753 years. So with period 8*(J,U)=110.5 years value L_w returns to ~0 ˚.

(V/3,-E/5,J/2) = 22.135 years = 110.68 years/5

Resonance E-R

Year	∆L_JU	L_ER[˚]
1278.11	-4	-2
1389.38	-1	-10
1499.69	-5	-8

(E,R/2) = (1.00000,1.88085/2) = 15.781 years = 110.47 years/7

Synchronization J-U a R-S?

Synodic period (R,S) = 2.009131627 fits (by 55 multiple) into 110.5 years period. 16.12.1920

Oppositions R-S coincide with oppositions J-U in years:
594.9, 705.47, 815.99, 926.48, 1036.96, 1147.48, 1257.98, 1368.46, 1478.97, 1589.47, 1699.95, 1810.46, 1920.96, 2031.45, 2141.95.
Some of the data (e.g.1699.95, 1810.46, 1920.96) point to periods with locally lower Solar activity. The last know decrease of solar activity is from the beginning of 20-th century.

Conjunctions J-X

Period 110.5 years coincide approximately with 9 conjunctions J-X (see Planet X)

9 * (J,X) = 9*12.2368 years = 110.13 years

E.g. 1686,12 ( 12,27) 1698,38 ( 12,27) 1710,65 ( 12,24)

1722,89 ( 12,27) 1735,15 ( 12,24) 1747,39 ( 12,24)

1759,63 ( 12,21) 1771,84 ( 12,21) 1784,05 ( 12,21)

1796,26

31.1.1686 13.6.1796

Cycle 221 years

Timo Niroma: „200-210 and 1000-1050 years seem to be the greatest known oscillation periods in Sun's intensity. They also seem to affect the temperature on Earth. During the last 400 years there seems to be a great resemblance between Wolfian numbers 221 years apart (the upper limit of the 200-year cycle?).“

220 years in the spectrum of solar activity.
220.55 years: 9*(U,N)/7 (anomalistic)
222.019 years: Wood’s moon tidal cycle (Fairbridge,1997).
222.6 years: ((J,S/2),U) = (60.85,83.75) (anomalistic)

Marked rainy periods

Zdenek Vasku has published (y.1997) detail analysis of rainy periods of the last millennium. He has pointed to existence of four marked periods (so called “little pluvials” I.-IV.) and predicted existence of the next period in years 1995-2035), see Our little pluvials. Period well fit into cycle 221 years:

Cycle 331.5 years = 2*165.75 years

Orbital period of Neptune corresponds approximately to 12 periods (J,U) and 13 periods (J,N) : 164.77 years: N

165.25 years: (W,J) = (11.06753, 11.861983), see Wood’s resonance
165.5 years ± 0.5 years: deviation of centers of mass Sun-JSUN and Sun-JS
165.75 years: 12 * (J,U) = 12*13.812; 166.17 years: 13 * (J,N) = 13*12.782
332.27 years: beats 4/(J,S) – 9/(S,U) = 4/J – 13/S + 9/U = 1/332.27 years
334 years: climatic cycle (Auric, 1936)

Cycle 442 years

Near approaches of Earth and Mars come approximately in intervals 47 years, 79 years, 205 years (=2*79+47), 284 years (=3*79+47) and so on. In sequence 1119,1198,1403,1482,1561,1640,1845,1924,2003, years 1119, 1561, 2003 (in distance 442 years) coincide with oppositions J-U. In this years Saturn pass perihelion, period 15*S =15*29.4572 years =441.86 years.

Cycle 554 years

Cycle of solar activity (intensive maxima) observed by J.Schove.

Cycle 884 years

Period 884.1 years is multiple of period 5*S, 884.1=6*147.35 years, 30*S=30*29.457=883.715 years, 64*(J,U) = 64*13.812 = 883.965 years, 139* I = 139*6.3611 years = 884.193 years. Ratio S/J corresponds to 149/60, so 30*S = 44.5 (J,S) = 74.5 J = 884.1 years.
Oppositions V-ER and at the same time opposition J-U occurs approximately in years: 17.7.235, 31.7.1119, 31.7.2003, 16.9.2887,…

23.10.1119 22.10.2887
syst11190813

Cycle 1216 years

According to analysis in project (Charvatova,Strestik) is significant climatic period equal to 1214 years. Let us note, that 1215.5 years = 11 * 110.5 years. Exact conjunctions V-E-R do not appear always after c. 300 years, period changes in span c. 298.9-318.2 years (298.9 years ~ 47*6.4-1.88 years, 318.2 years ~ 50*6.4-1.88 years). E.g. we find E-V-R in one line in years 1044.05,1343.00,1661.19,1960.13,2259.09; difference 2259.09-1044.05=1215.04 years.

Cycle 1768 years

According to 1767.4 years: 2*883.7 years=3*589.1 years = 17* 103.96 years = 89 * 19.859 years . (If in conjunctions V-E-R one period of Mars drop out after c. 300 years, it is like one Wolf’s period during 1768 years…)

Stadial cycles

In connection to cycles of ice ages (stadial cycles) mainly triad of periods 550 years–1100 years–1650 years was alluded. Reflection of multiples of c. 280 years period in climatic oscillations (Stacey, Karlstrom,..)

Cycle of 280 years

278.0304 years: 14SJ/EV (Fairbridge,1997)
280 years: biologic cycle (tree rings)
280.054 years: 2*140.027 years
283.0 years: glacier-iceberg changes
284.7075: Mayan cycle, part of Babylonian cycle, 24*J= 2*B/3 = 400 tzolkin (151 R)
285.0 years: (32.87, S)
286.1 years: E-R cycle, 7* 40.876 years
286.96 years: 8*(S,N) = 8*35.87 years
290 years: solar cycle (old Chinese observations)

Five-fold motion of the Sun?

For sidereal periods of outer planets the following equation holds (see Stable resonance ):

3/J-8/S-2/U+7/N = 0

Two analogous relations 8/S-3/J=5/G and 7/N-2/U=5/G compose equation (8/S-3/J) - (7/N-2/U) = 0, that holds precisely, at least for average periods. Hence G=267.67-267.78. Is it possible that motion of Sun-J-S makes pentagon instead of trigon (with regard to notional period G…) according to resonance S:J not 5:2, but 8:3 ? With regard to period G=270-285 years synodical periods (S,G):(J,G) makes ratio 8:3; (J,G)=12.4 years (see P.Kalenda,J.Málek: theory of solar dynamo) (S,G)=33.0 years (3 Wolf’s cycles).

Indicia for five-fold motion

c. 2003.7 (18.8.2003-31.8.2003) when planets aligned to line according to minimal interaction, spacing of Jupiter and Saturn was c. 54˚, i.e. (360˚+180˚) /10. Landscheidt’s five-fold property observation of c. 270-ti years period in tidal theory (see P.Kalenda,J.Málek: theory of solar dynamo) observation of shifts of 180 years cycles with synchronization each 2*270 years (P.Kalenda)

Stacey‘s cycle

536.2 years: 3*178.73 years
536.2 years: mutual motion J-S-Hidalgo, 7* 76.6 = 7*(J,Hidalgo) = 20*26.81 = 20*(S,Hidalgo),
537.0 years: beats 3/J-2/V+3/E
540-580 years: Pearson’s-Stacey’s cycle
550.0 years: Feirbridge’s cycle 550,1100,1650 (3600) years
556 years: Stacey’s - Zero-check cycle/3, (539.8-556.0, mean 548 years)
556 years: multiple of conjunctions J-S (28*19.86=3*185.3)
556.027 years: advance of moon perigee (Fairbridge, Sanders)
556.0609 years: SQ-1 (Fairbridge,1997)
558 years: moon tidal cycle (Wood)
560 years: S-U perturbations (Schlyter)
566.58 years: (S,U/3) (anomalistic)
567 years: Pearson’s geologic cycle
570 years: temperature cycle, geologic cycle (sandstone formations)

Karlstrom‘s stadial cycle

1000 years climatic cycle
1112 years: Stacey’s cycle, (anomalistic)
1118.23 years: Jakubowski - model of solar activity
1133.0 years: Karlstrom’s stadial cycle

Petterson‘s tidal cycle

1665.7 years: 9/25 *4627 years = 9* 185.08 years
1668.1825 years: SQ-3 (Fairbridge,1997)
1668 years Stacey’s Zero-check cycle 3*556 years, Earth-Moon, 84*(J,S)
1700.0 years: geophysical cycle of iceberg changes; motion of icebergs (Pleistocene)
1703.5 years: inequalities (544.79,800.94) (tropical periods)
1708 years: 5125 years/3 (cycle derived from Mayan), 4*B = 144*J=1708.245 years
1708 years: eruptions of volcanoes (-3341 Avelino,-1633 Thera,+75 Vesuvius,+1783 Laki)

Karlstrom's great cycle

3336.365 years: SQ-6 (Fairbridge,1997)
3400.0 years: Karlstrom’s cycle of ice ages