Music theory - Harmonic statics
Root
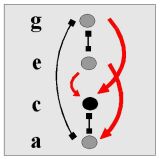
Chord
Chord is a combination of two or more tones.
Distance of any two tones can be meassured.
Generally, chord as parallel sound of n tones (n-sound)
is composed of N = n ∙ (n-1) / 2 intervals (bindings).
E.g. 2-sound from a one interval, 3-sound of three and 4-sound of the six intervals.
Idealized chord - to each tone all audible octaves - but not aliquote or differential tones (?)
Zarlino Gioseffo| Zarlino Gioseffo , 1517-1590, Italian Renaissance composer and music theorist regarded as founder of the theory of harmony. He tried to get music theory away from mysticism. He elaborated theory of vocal counterpoint Renaissance polyphony. He treats all musical components (harmony, melody, metrics, rhythm, ..) and their relationships. He considered as basic chords the major and minor triad. |
Tone grouping
We call formal chord the chord, that abstracts from octave identity.
E.g. formal chord [c,e,g] stands for the chord [e1,g1,c2] and chord [c1,g1,c2,e2 g2], generally any multi-sound composed of tones c1,c2,...,e1,e2,...,g1,g2,...
Formal chord tones is a subset of the formal system and representative of all the harmonies which have the same formal structure..
Because a large part of the text is dedicated just only to formal relationships, we will (if it will not depend on the accuracy of the definition) speak generally about tonal harmonies or clusters.
Skuherský František Zdeněk| Skuherský František Zdeněk ,-, Czech music theorist. He brought a new concept of harmony both from theoretical and methodological point of view. He refused Riemann functional system and sought to get rid of older prejudices (construction of thirds chords, ...). He coniders each vertical cross section of a music composition as chord, the basis of chords are intervals. He has classified the chords according to the number disonant intervals. |
Characteristics of chords
Continuity of n-sound C is the average of absolute values of the continuity in individual links.
C = øc = ∑|c| / N
Impulse of n-sound I is the average value of the impulses in individual links:
I = øi = ∑i / N
Major and minor triad have the same value of continuity and impulse:
C = (c1+ c2 )/3 I = (i3+i4…)/3
Given a connection matrix of continuity C (or matrix of the absolute values |C|) and matrix of impulse I, then characteristics of the chord are determined by relations:
C(u)=u∙|C|∙u, I(u) = u ∙ I ∙ u
where u represents a binary structure (vector) of the chord.
Mersenne, Marin| Mersenne, Marin [mersen], 1588-1648, French monk - mathematics, music theorist and philosopher. One the most important linkages of science of the 17th century. He derived sonance of intervals and chords from numerical ratios. He showed that there is no need to consider bas as a basis for the vertical structure, substantial is relationship of tones. |
The root
The tone is considered as the root (the basic tone) of a chord, if it stand out most of all tones in the foreground, respectively if man will most likely sung it to the chord.
According K.Risingera is the root such tone that we do not feel dependent on another (real or imaginary) tone. Isolated tone has tendency to be basic, other tones that tendency promotes or cancels. Prof. Risinger also describes the conditions determining "dependency" of tones. (From these conditions we will further derive values of continuity.)
The tone of the most energetic band is not necessarily a tone with greatest acoustic energy. It is the tone that gets more power - ie. the tone deeper if possible, into which leads most of the links of continuity.
The root of the chord is tone to which the band with the maximum rootness (ie. a real energy of band) corresponds. Rootness is the probability that the tone will be marked as the root.
(This energy does not depend on the modality and its potentials.)
The root is such an tone that the most energy receives and at the same time as little as possible energy transmits.
The root is the tone matching to band with maximum energy. It passes small amount of energy to other tones and it receives a large amount of energy.
Tone with E = max(Ei), it is tone, which other tones support;
E.g. both tones {g,e} of chord [c,e,g] send part of its energy to tone {c}. Tone {c} becomes root of the chord [c,e,g].
Chord may have more than one root. (But if all bands have the same energy,
it have no root). Chord may also have an imaginary root, i.e. the root
outside of chord tones.
E.g. chord [e, f, g] has imaginary root {c}. Both tones {e, g} transmit energy
to {c} and tone {c} is disturbed by no sounding tone.
Impulse bindings e-f and f-g cancels all chord tones [e, f, g].
The root can be defined in various ways. To understand the different possible concepts we will distinguish the following types of roots:
Internal - part or sounding chord.
Modal - part sounding modality (may not be included in the chord)
System - part of the tonal system (may be outside modality).
Serre Adam| Serre Adam [], 1704-1780, He identified the fundamental bass with major triad, he pointed out that a complete acoustically-justifiable interpretation of the four-tone chord needs two fundamental bases, for example: d-f-a-c / F+G. |
Acoustic - may be out of tone system.
rootness zi=1; entropy: w =–i zi log zi
- energy E = Q + W ( input E tones, output Q - bands, W - bindings
(+entrop of the structure).
When the chord has sharply defined root, then it has a low entropy and positive genus (see below)..
Sonance and genus
Effect of chords
|
Chord |
Schema |
∑c |
∑i |
C |
I |
Difference |
|
Enlarged |
44(4) |
3c2 |
3i4 |
3.00 |
0.50 |
2.50 |
|
Major |
43(5) |
c1+ c2 |
i3+i4 |
3.00 |
0.83 |
2.17 |
|
Minor |
34(5) |
c1+ c2 |
i3+i4 |
3.00 |
0.83 |
2.17 |
|
Quart |
52(5) |
2c1 |
i2 |
4.00 |
2.17 |
1.83 |
|
Diminished |
33(6) |
0 |
2i3 |
0.00 |
1.33 |
–1.33 |
To determine the approximate effect of chords can serve the difference of values continuity and impulse P = C –I.
The value of continuity rather increases and the value of the impulse decreases sonance amount of the chord.
K.Janeček has work with the characteristics of the consonance of chords similarly.
Risinger Karel| Risinger Karel , -, Czech music theorist and educator. He dealt with the theory of modern harmony a general hierarchy of musical units. Tried to extend Šín's functional system by relationships of all chords to the tonic. Defined conditions for determining roots of chords. Published treatise about micro-interval systems. |
- chords somehow differ in their effect => property-sonance - the degree of inner tranquility (x external tranquility - potential) - consonance - orderliness allows the system stay longer in a given state = > high incidence in the songs (classical). - x5+ - is dissonant not due to frequency ratios, but due to tone qualities (?) - exists only within the system, modality - it can can act quite the opposite in another modality, derivation from the potentials. - ability to operate under certain circumstances without the feeling of tension (dissonant chord may be in the context consonant?) - dissonance dampens - by adding consonant components
Polarity of major and minor
The distribution of links in major and minor triads differ:
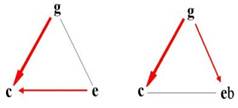
| Major 43(5) | |||
| c | e | g | |
| –c1 | i3 | 0 | g |
| c2 | 0 | i3 | e |
| 0 | –c2 | c1 | c |
| Oettingen Artur Joachim von [], 1836-1920, was looking for arguments to justify the acoustic equivalence of major and minor chord. Complex chords arise by mixing of aliquots, the simplest mixing is just in the case of the major and minor triad. He assumed originally also lower overtone serie. |
We're talking about ordering of maxima and minima. This orderliness is called genus.
Consonance of the major chord CEG consists of two links continuity to the tone C (EC a GC).
| Minor 34(5) | |||
| c | es | g | |
| –c1 | -c2 | 0 | g |
| i3 | 0 | c2 | es |
| 0 | i3 | c1 | c |
A minor chord is consonant CEbG because it is similar to a minor third. Tone G loses a lot of energy through two links of continuity of tone G (GC and GEb).
Major and minor chord sounds good in close position, because the both continuity links are pointing downward. Due to the fact that the sound of the major chord will not be worsen by lowering the tone C (in the lower octaves) it has been suggested that the same applies to the increase of tone G in the minor chord.
Genus
Genus of tone groupings depends on the distribution of energy between the bands.
It is property of best arranged chords.
Positive genus corresponds to grouping with a marked maximum (I.),
negative genus to grouping with a marked minimum (II.).
A simple algorithm to determine an approximate genus. Let t is the tone of chord with the largest (not oriented) potential. Then genus G of the chord is:
G(u) = Ep(t) ∙ signum(Er(t)), where signum() is function returning –1,0 or +1.
Hauptmann M.| Hauptmann M. [], -, sought to justify the acoustic equivalence major and minor chord. |
Redistribution of energy
Let us denote energy of a tone i in the chord u by E(u, i).
We assume two types of potential energy - the non-oriented energy Ep
and directional (basic) energy Er.
Let us consider the following relations:
Ep(u,i) = ∑(|C(h(i,j))|,j) – ∑(I(h(i,j)),j)
Er(i,u) = ∑(C(h(i,j)),j) – ∑(I(h(i,j)),j)
where h(i,j) is formal distance (interval) of tones i,j;
C is continuity, I impulse.
So vektors of energy E(u) of all tones are:
Ep(u) = u.(|C|–P), Er(u) = u.(C–P),
C is matrix of continuity, I is matrix of impulse.
| Chord | Schema | t | Ep(t) | Er(t) | Genus |
| Increased | 44(4) | - | +4 | 0 | +4 ∙ 0 = 0 |
| Major | 43(5) | c | +6 | +6 | +6 ∙ +1 = +6 |
| Minor | 34(5) | g | +6 | –6 | +6 ∙ –1 = –6 |
| Quart | 52(5) | c | +8 | 0 | +8 ∙ 0 = 0 |
| Diminished | 33(6) | - | –1 | –1 | –1 ∙ –1 = +1 |
Both chords have a root c, [9] which is somewhat stronger in the case of major triad (E = + 6) than in the case of the minor (E = + 4). Major triad has extreme value of rootness positive (E = + 6) while minor triad negative (E = -6). Clarity of major lies in the extremely high rootness of tone c, while blurring minor in extremely low rootness of tone g, while the entropy (dissonance) of both units is approximately the same.
Inverse chords
Chord is an inversion of given chord if it has the same interval structure in reverse order. E.g. chord Hmi7 is inverse of chord G7:
The number of intervals (0-6):
0 1 2 3 4 5 6
----------------------------
G7 4 0 2 4 2 2 2
Hmi7 4 0 2 4 2 2 2
g h d f a f d h
------------- --------------
2 6 3 0 f 2 6 3 0 h
5 3 0 3 d 5 3 0 3 d
4 0 3 6 h 4 0 3 6 f
0 4 5 2 g 0 4 5 2 a
The flow of energy (in the formal system) is the same in chord and in its inversion. This helps us to monitor the characteristics of chords (one root, entropy, ..).
Inverse intervals:
1(11)-11(1); 2(10)- 10(2); 3(9) - 9(3); 4( 8)- 8(4); 5( 7)- 7(5);
Inverse triads:
12(9) - 21(9); 13(8) - 31(8); 14(7) - 41(7); 15(6) - 51(6); 23(7) -
32(7);
24(6) - 42(6); 34(5) - 43(5);
- inversion chords - the same level of dissonance, but not used equally
Music entropy
The concept of entropy comes from physics and indicates the degree of disorder. Consider two tanks - one with hot and the other with cold water. It is an balanced state - we know that all faster molecules are in the container with warm water, while all the slower molecules in the second container. Mixing of water causes disorder i.e. increase of entropy of the all system.
Clausius Rudolf| Clausius Rudolf Julius Emanuel [klauzijus], 1822-1888, German physicist, formulated 2.termodynamic theorem, contributed to building kinetic theory of gases. He introduced the concept of entropy. |
Energy and enthropy
Energy E = Q + W - input E - tones, - output Q - bands ( potentials ) W - bindings. Sounding of chord draws energy from W. To greater entropy, more energy is needed w - W. Bands have q∙t; bindings take w∙t. Entropy as the sum of interference from all the beats between aliquots (Knopoff, Hutchinson).
Definition of entropy
Mathematically, entropy is defined by the equation (for i=1..k, ∑pi=1
H = –∑(pi∙log(pi))
This relationship is also used in information theory. In the following examples, we calculate with the natural logarithm (base e).
Let us have two phenomena with approximately the same characteristics, for example 0.45 and 0.55.
then H = – (0.45 log 0.45+ 0.55 log 0.55) = 0.688
If we are not able to distinguish that phenomenon is better or more significant, the entropy is higher (we are starving, because we are not able to choose food,...) Otherwise, if we have two events with characteristics e.g. 0.9 and 0.1,.., we know for sure what to choose, and entropy is low:
H = – (0.9 log 0.9+ 0.1 log 0.1) = 0.325
Entropy of chord
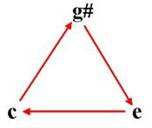
The degree of disorder, the entropy of chord (disonance) depends on distribution of energy between the bands. The smallest enthropy is in chord with clear root tone and largest enthropy has chord if energy of all its tones is balanced.
So called genus can be seen in the best-ordered groupings. Two poles of the genus corresponds to the two types of arrangement; arrangement with a marked maximum corresponds to the positive genus, arrangement with a marked minimum to negative genus.
| - | c | e | g# | E |
| g# | 0 | +2 | –2 | 0 |
| e | –2 | 0 | +2 | 0 |
| c | +2 | –2 | 0 | 0 |
Entropy of chord depends on the distribution of power between the bands. Maximum entropy appears when the energy of all tones are balanced. Entropy is therefore similar to the uncertainty in the determination of the root. The term 'entropy' is used as a synonym for 'amount of dissonance'. Consonant chords have a low entropy, dissonant chords a high entropy.
Imperfection of the consonance of the augmented triad ceg#. [6] Energy of this triad are balanced. The cause of imperfect consonance could be higher entropy.
Influence of intensity of tones
Considerations on rootness of a tone usually refer to the tones with the same intensity.
Consider now how rootnes of the individual chord tones could be affected by the sound intensity. Suppose that continuity c1 moves 50% and c2 25% of total energy production, i.e. of power [Watts]. Let minor triad A,C,E is a sounding with energy distribution A (20%), C (20%), E (60%), i.e e.g with a total power of 100 mW sounds A (20mW), C (20mW), E (60mW).
Because 50% of energy E goes to A (E=>A) and 25% energy E goes to C we get (after redistribution that occurs at the moment of hearing the tone):
E 60mW –(50% of 60mW) –(25% of 60mW) = 60mW–30mW–15mW = 15mW C 20mW +(25% of 60mW) = 20mW +15mW = 35mW A 20mW +(50% of 60mW) = 20mW+30mW = 50mW
Tone A becomes the root of A-C-E. But with the initial distribution A (20mW), C(40mW), E(40mW) tone C becomes to be root:
E 40mW –(50% z 40mW) –(25% z 40mW) = 40mW–20mW–10mW = 15mW C 40mW +(25% z 40mW) = 40mW +10mW = 50mW A 20mW +(50% z 40mW) = 20mW+20mW = 40mW
In these examples - the tone E reminds watering can which has two bottom holes. (to tone A and to tone C). The production of tone E corresponds to pouring water to this can.
(The continuity is bound to another question. When sounding chord CFG - tone G gives some energy to tone C. Does tone C give also part of this new energy to tone F?!)
Sonance and information value of harmony
Similarly, as about the energy of the water we can think about energy in tone bands. When energy of tones is balanced entropy increases.
Shannon Claud Elwood| Shannon Claud Elwood [šenon], 1916-, American mathematician, engaged in information theory and applications of communication and computer technology. |
If we define rootness as the probability that the tone will be used as the root, then entropy corresponds to a measure of dissonance of chord. Consonant intervals and chords must have a very strong root.
Information is the amount of something (energy), which removes the uncertainty.
derived from the system disorder
- rootness zi=1, the probability zi - that an event (determination of a given tone as the root) occurs
-information contained in the phenomenon(?) Ii= ln zi
- entropy, míra neuspořádanosti: w =–i zi Ii=–i zi log2zi = –log2e ziln zi
- informační tok i = I/t – w/t - redundance - how many % remains to achieve total dissonance; - consonance - orderliness enables system to last longer in the given state => high incidence in the songs (classical).
Sonance and thermodynamics
Arrangement - there is little number of elements, that look the same from the outside, (low number of transpositions of the class) => (order is only one but there are plenty disorders)
(=> information - the number of possible transpositions (of a class) of communication! - T=0 => w=0 (all perfectly arranged) When delivered heat dQ to system with temperature T w of the system increases by dw=dQ/T (?)T=0,...
Harmonics and differential tones
To accurately determine the root, we should count with both harmonics as well as differential tones. E.g. in the chord C-Eb-B the fundamental tone Ab comes into consideration. There are 2 links of Eb leading to the tone Ab. => Ab a C => Ab. But can we say that the minor third C-Eb has the (imaginary) keynote Ab? (It depends on the exact definition of the root, but we do not have it.) According to prof.Janeček is for a listener always difficult to understand eg. tone F as a root of minor third A-C, when the tone F does not sound. Fundamental tone F = nsd(880 Hz,1056 Hz) = 176 Hz = 704 Hz/4 is two octaves below the given tones.
Formal resonance
Basic definitions
Let f2/f1= n2/n1, where n1,n2 ε N (integers) and let q=f2/n2=f1/n1.
Fundamental frequency f0 is defined:
f0=q*n0, where n0=gcd(n1,n2), gcd is greatest common divisor.
The given tones (f1,f2) are aliquots of the fundamental tone
(f0).
Common frequency f is defined:
f=q*n, where n=lcm(n1,n2); lcm is lowest common multiple.
Let frequency ratios of a given chord are f1/f2/f3,... =
n1/n2/n3,..., where n1,n2,...ε N (small integers).
We will call resonant characteristic n of chord the lowest
common multiple of all numbers n(i),
n = lcm(n1,n2,n3,...).
Let formal period r=r(n) is natural period of number n without prime 2 in factorization (octave identity).
Formal resonance of intervals
In the following table are the resonant characteristics n and their formal periods r:
| Interval | n1/n2 | Primes | Characteristic n | Formal period r |
|---|---|---|---|---|
| 0 | 1/1 | 1,1 | 1 | 1 |
| 7 | 3/2 | 2,3 | 6 | 3 |
| 5 | 4/3 | 22,3 | 12 | 3 |
| 4 | 5/4 | 22,5 | 20 | 5 |
| 8 | 8/5 | 23,5 | 40 | 5 |
| 9 | 5/3 | 3,5 | 15 | 15 |
| 3 | 6/5 | 2,3,5 | 30 | 15 |
| 6 | 7/5 | 5,7 | 35 | 35 |
If we feel e.g. interval 5/4 as consonant, then we "understand" prime 5.
Number 4= 2*2 is received "automatically" (octave identity).
All (formal) intervals of 12-tone system:
| Interval | Ratio | Fraction n1/n2 | Formal fraction | Formal period r |
|---|---|---|---|---|
| 0 | 1.00000 | 1/ 1 | 1/ 1 | 1 |
| 1 | 1.06667 | 16/15 | 1/15 | 15 |
| 2 | 1.12500 | 9/ 8 | 3/ 1 | 3 |
| 3 | 1.20000 | 6/ 5 | 3/ 5 | 15 |
| 4 | 1.25000 | 5/ 4 | 5/ 1 | 5 |
| 5 | 1.33333 | 4/ 3 | 1/ 3 | 3 |
| 6 | 1.40000 | 7/ 5 | 7/ 5 | 35 |
| 7 | 1.50000 | 3/ 2 | 3/ 1 | 3 |
| 8 | 1.60000 | 8/ 5 | 1/ 5 | 5 |
| 9 | 1.66667 | 5/ 3 | 5/ 3 | 15 |
| 10 | 1.77778 | 16/ 9 | 1/ 3 | 3 |
| 11 | 1.87500 | 15/ 8 | 15/ 1 | 15 |
| 12 | 2.00000 | 2/ 1 | 2/ 1 | 1 |
According to this table the halftone has the same formal period (15) as the minor third. The triton has highest formal period (35).
Dissonance of the halftone is caused by impulse characteristic of this interval.
Formal resonance of chords
Ratios of a three selected triads:
Major [c,e,g] Minor [c,eb,g] Augmented [c,e,g#]
n1/n2/n3 = 2/3/5 n1/n2/n3 = 6/10/15 n1/n2/n3 = 1/5/25
-------------------------------------------------------------------------
f2= 3 f3=15 f3=25
g g g#
3 3 3 5 1 5
1 5 1 1 5 1
c e c eb c e
1 5 5 3 1 5
f1= 2 f3= 5 f2=10 f1=6 f1=1 f2=5
-------------------------------------------------------------------------
n=lcm(2,3,5)=30 n=lcm(6,10,15)=30 n=lcm(1,5,25)=25
r=r(30)=15 r=r(30)=15 r=r(25)=5
Augmented triad has lower formal period (5). If we feel it to be more dissonant than major or minor triad, it is because we are not able reduce 52 to 5 ("exponential identity").
Euler's theory
Let rational number qεQ has prime factorization:
q = product(p(j)a(j)), p(j)εP (primes), a(j)εZ (integers).
The "gradus suavitatis" (degree of sweetness) of q is:
G(q) = 1 + a(1)*(p1-1) + a(2)*(p2-1) +.... + a(n)*(pn-1).
Single octave (21) is removed from computations (1*(2-1)=1), but octave identity as a whole is not removed.
Some theorists (J.Jeans, J.Volek,..) criticized the Euler theory of
consonance.
They objected e.g. that the chord (f,a,c,e) gets the same
characteristic as the chord (f,a,c,f).
The formal periods of these chords are also the same:
n(f,a,c,f) = lcm(4,5,6,8) = 120
n(f,a,c,e) = lcm(8,10,12,15) = 120
r(f,a,c,f) = r(f,a,c,e) = r(120) = r(23*3*5) = 15
Dissonance of the chord r(f,a,c,e) is caused by impulse characteristic of interval e-f.