Schematic algebra - Segmentation
Segments of systems
The nesting (shown in the previous paragraphs) is a matter of G-systems with constant n. Now we are going to study G-systems with constant k.
G(2,2) => G(3,2)
0 0
1 2 1 3
3 4
6 2
7 5
8
Definition of segments
Each G-system can be divided to segments in the following way. New instances will be separated from instances of G-system of lower n.
E.g. let us observe the systems G(2,2) and G(3,2). The latter is only an extension of the former.
Every G(n,k) has n classes nested from G(n,1). Let us assume that these classes divide G-system into segments.
In segment s (s<n) has every such class number:
g(s) = (n−s) ∙ (nk−1) / (n−1)
To any segment existing in G(n,k) there exist a similar segment in G(n+1,k). This idea becomes clearer if we rewrite all numbers u with numbers (nk-1)-u.
At the same time we renumber segments to s'=(n−s).
E.g. segments in G(3,3):
u:
0
segment 2
1 3 9
2 6 18
4 12 10
5 15 19
7 21 11
8 24 20
──────────────────
13
segment 1
14 16 22
17 25 23
──────────────────
26
segment 0
|
u':
0 segment 0'
──────────────────
9 1 3
12 10 4
13
segment 1'
──────────────────
18 2 6
19 5 15
21 11 7
22 14 16
24 20 8
25 23 17
26
segment 2'
|
Numeric systems
Let us write the numbers nk-1-u from the previous table as functions of n and look at quotients of the polynomials.
Numbers nk−1−u from the previous table as functions of n:
k=2 k=3
segment 0 segment 0
1 1
segment 1 segment 1
n 1 n2 1 n
n+1 n2+n n2+1 n +1
n2+n+1
Let us write coefficients of these functions (polynomials):
k=2 k=3
segment 0 segment 0
0 0 0 0 0
segment 1 segment 1
1 0 0 1 1 0 0 0 0 1 0 1 0
1 1 1 1 0 1 0 1 0 1 1
1 1 1
Each G-system is a set of numbers from the n-th numeric system.
| The G-relation separates G(n,k) into n segments, where every segment s uses always just s symbols, s=0..n-1. |
Sum of coefficients of polynomials is the same as for all instances of given class (instance of the same class have the same level).
Compositions of G-systems
Example of G(n,2)
G(1,2) 00 00 00
─────────────────────────
10 01 10 01 10 01
G(2,2) 11 11 11
─────────────────────────
20 02 20 02 20 02
21 12 21 12 21 12
G(3,2) 22 22 22
─────────────────────────
30 03 30 03
31 13 31 13
32 23 32 23
G(4,2) 33 33
─────────────────────────
40 04
41 14
42 24
43 34
G(5,2) 44
|
Example of G(n,3)
G(1,3) 000 000 000
────────────────────────────────────────────
100 001 010 100 001 010 100 001 010
110 101 011 110 101 011 110 101 011
G(2,3) 111 111 111
────────────────────────────────────────────
200 002 020 200 002 020
201 012 120 201 012 120
210 102 021 210 102 021
211 112 121 211 112 121
220 202 022 220 202 022
221 212 122 221 212 122
G(3,3) 222 222
────────────────────────────────────────────
300 003 030
301 013 031
302 023 032
310 103 130
311 113 131
312 123 132
320 203 230
321 213 231
322 223 232
330 303 330
331 313 331
332 323 332
G(4,3) 333
|
Electron peels in atoms
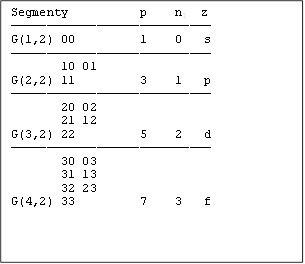
Number of electrons p in peel having auxiliary quantum number nl corresponds to number of instances in nl−th segment of G-systems of order k=2. (In the column z is usual denotation of peels).
Self classes
Number of self classes in segments is difference of numbers of self classes of two systems with adjacent bases, i.e.:
s(n,k) = v(n+1,k)−v(n,k)
Numbers of self classes in segmentsNumbers of self classes in segments s(n,k) written as functions of variable n:
k m(n,k) ──────────────────────────── 1 1 2 n 3 n∙(n+1) 4 (n/2)∙(2n²+3n+1) 5 n∙(n³+2n²+2n+1) 6 (n/6)∙(6n4+15n³+20n²+12n+1) 7 n∙(n5+3n4+5n³+5n²+3n+1) 8 (n/4)∙(4n6+14n5+28n4+35n³+26n²+11n+4) |
0 1 2 3 4 5 6 7 ───────────────────────────────────────── 1 1 1 1 1 1 1 1 0 1 2 3 4 5 6 7 0 2 6 12 20 30 42 56 0 3 15 42 90 165 270 423 0 6 42 156 420 930 1806 3192 0 9 107 554 1910 5155 11809 24052 0 18 294 2028 8820 28830 77658 181944 0 30 780 7350 40590 161040 510510 1376340 |
(Computation of s(n,4) is known as: 3= 1+2; 15= 4+5+6; 42= 9+10+11+12; 90= 16+17+18+19+20).
All classes
Similarly as in the previous paragraph:
t(n,k) = m(n+1,k)−m(n,k)
Numbers of classes in segmentsNumbers of all classes in segments t(n,k) written as functions of variable n:
k t(n,k) ───────────── 1 1 2 n+1 3 n²+n+1 |
0 1 2 3 4 5 6 7 ───────────────────────────────── 1 1 1 1 1 1 1 1 1 2 3 4 5 6 7 8 1 3 7 13 21 31 43 57 |
All instances
Similarly is also:
S(n,k) = M(n+1,k)−M(n,k) = (n+1)k−nk
Kronecker Leopold| Kronecker Leopold, [] 1823-1891, German scholar and mathematician associated with the idea of arithmetization of mathematics, opponent of Cantor's concepts. He was interested in arithmetic of quadratic forms, theory of ideals and elliptic functions. Refused actual infinity. All mathematics have to be based on numbers and all the numbers on the natural numbers: "The natural numbers are from God, the other is the work of man." |
Numbers of all instances in segments S(n,k) written as functions of variable n:
k S(n,k) ───────────────── 1 1 2 2n+1 3 3n²+3n+1 4 4n³+6n²+4n+1 |
0 1 2 3 4 5 6 7 ───────────────────────────────────── 1 1 1 1 1 1 1 1 1 3 5 7 9 11 13 15 1 7 19 37 61 91 127 169 .... |
Number S(n,k) (called also Kronecker’s delta) – has relation to Bernoulli’s sequences (see Triangles) and to Last Fermat’s theorem.
Periodic sequences
Period of sequence
Let us consider sequence of numbers an. If there exist such number r, that for all n it holds an+r = an, then {an} is so called periodic sequence. Number r is period of sequence.
Least period of the given sequence is basic (natural) period.
Members of differential sequences
Generally r-th member of s-th differential sequence
|
as,r = ∑(−1)i ∙
|
(sum for i=0..s)
In sequences of cubes is:
s\r 1 2 3 4 5 6 ... ──────────────────────────── 0 0, 1, 8,27,64,125,... 1 1, 7,19,37,61,... 2 6,12,18,24,... 3 6, 6, 6,...
a2,3 = ∑(-1)i a3+2-i =
![]() a5 -
a5 -
![]() a4 +
a4 +
![]() a3
= a5-2a4 +a3 = 64 - 2*27 + 8 = 18
a3
= a5-2a4 +a3 = 64 - 2*27 + 8 = 18
In sequence of order s is s-th differential sequence
constant, i.e. every number of this differential sequence equal to
0-th member:
as,0 = ∑(−1)i
![]() as−i = Ks .
as−i = Ks .
In case Kp= p! = 0 mod p (pεP) analogically it holds:
ai+p + (−1)p ai = 0 mod p
E.g. p-th power: (i + p)p + (−1)p ∙ ip = 0 mod p.
For p = 2: a0 = 0; a1 = 1;
a2 = 4; a3 = 9; a4 = 16;
a5 = 25; a2+a0= 4,
a3+a1 = 10 is 0 mod 2.
For p = 3: a0 = 0; a1 = 1; a2 = 8;
a3 = 27; a4 = 64; a5 = 125;
a3−a0= 27, a4−a1 = 63
is 0 mod 3.
If pεP, tak it holds Wilson’s theorem: K(p)=(p−1)! ≡ −1 (mod p).
For every i = 1..p−1 is
![]() = 0 mod p.
= 0 mod p.
The first and last member rests: a(p) + (−1)p ∙ a0 = −1 (mod p)
Because all members of p-th differential sequences equal, we can select other member, i-th (instead of 0-th):
a(i+p) + (−1)p ∙ ai = −1 (mod p)
Natural period
Let qεQ has prime partition: q = ∏ (pjaj), pjεP, ajεZ. ¨
n\k 1 2 3 4 5 6 7 8 9 10 11 12 ─────────────────────────────────────── 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 1 1 1 1 1 1 1 1 1 1 2 0 0 2 0 2 4 2 0 8 4 2 4 3 0 1 0 1 3 3 3 1 0 9 3 9 4 0 0 1 0 4 4 4 0 1 6 4 4 5 0 1 2 1 0 1 5 1 8 5 5 1 6 0 0 0 0 1 0 6 0 0 6 6 0 7 0 1 1 1 2 1 0 1 1 9 7 1 8 0 0 2 0 3 4 1 0 8 4 8 4 9 0 1 0 1 4 3 2 1 0 1 9 9 10 0 0 1 0 0 4 3 0 1 0 10 4 11 0 1 2 1 1 1 4 1 8 1 0 1 12 0 0 0 0 2 0 5 0 0 4 1 0 ─────────────────────────────────────── R 1 2 3 2 5 6 7 2 3 10 11 6
Number: R = ∏pj is called natural period.
Number of residual classes of expression nk mod k, n,kεN0, is equal to natural period R of number k.
Natural classes
Natural classes in G-system
Let us order instance of each class of G-system into
ascending sequences. If all differences of instances {d1,d2,...}
have form
B∙(nj), j=0..k−1,
we speak about natural class (N-class).
Differences {d1,d2,...} in G(n,k) are always divisible by
n−1.
Diference of instances
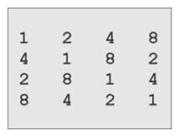
Construction of natural classes in G(2,4)
Instances Ordering Differences Type Nb ──────────────────────────────────────────────────────── 0 0 x − 1 2 4 8 1 2 4 8 1 2 4 N1 3 6 12 9 3 6 9 12 3 3 3 − 5 10 => 5 10 => 5 − 7 14 13 11 7 11 13 14 4 2 1 N1 15 15 x −
In system G(2,5), are all self classes natural.
Instances Differences Type Nb ──────────────────────────────────────────────────────── 0 − − 1 2 4 8 16 1 2 4 8 N1 5 9 10 18 20 => 4 1 8 2 N1 11 13 21 22 26 2 8 1 4 N1 15 23 27 29 30 8 4 2 1 N1 31
Type natural class mark Nb, where b = B/(n−1). For n=2 is B=b=1 (examples above); for n=3, is B=2,4 a b=1,2; for n=4, is B=3,6,9 a b=1,2,3; and so on.
Outlines
G(2,2): x G(3,2): x G(4,2): x
1 P 2 P 3 P
x 4 P 6 P
k=2; φ(2) = 1 x 9 P
2 P x
x 3 P
6 P
x
3 P
x
G(2,3): G(3,3): G(4,3):
x x x x
1 2 P 2 6 P 3 12 P 3 12 P
2 1 P 4 12 P 6 24 P 6 24 P
x 6 2 P 9 36 P 12 3 P
10 4 12 3 P 18 9
4 10 18 9 9 18
k=3; φ(3) = 2 12 4 P 21 21 24 6 P
x 9 18 x
2 6 P 24 6 P 3 12 P
6 2 P 33 6 12 3 P
x 6 33 x
21 21
36 9 P
G(2,4): G(3,4):
x x 40
1 2 4 P 2 6 18 P 12 4 28
3 3 3 4 12 36 P 24 14 8
5 8 16 8 10 30 10
4 2 1 P 10 30 10 36 12 4 P
x 14 8 34 x
16 32 16 2 6 18 P
k=4; φ(4) = 2 20 8 16 8
8 14 24 20
18 6 2 P 18 6 2 P
28 4 12 x
16 16 16
34 8 14
Differences of natural classes make some latin squares and similar figures:
k=2: 1 k=3: 1 2 k=4: 1 2 4 k=5: 1 2 4 8
2 1 4 2 1 4 1 8 2
2 8 1 4
8 4 2 1
k=6: k=7: k=8:
1 2 4 8 16 1 2 4 8 16 32 1 2 4 8 16 32 64
16 8 4 2 1 8 1 16 2 32 4 4 32 1 8 64 2 16
16 4 1 32 8 2 16 2 64 8 1 32 4
2 8 32 1 4 16 64 32 16 8 4 2 1
4 32 2 16 1 8
32 16 8 4 2 1
Identification of classes
For numbers N-classes g(j) v G(n,k) it holds:
(nj−1)∙g(j) mod (nk−1) = b∙(n−1)∙nj−1
where nsd(j, k) = 1.
Symbol b marks number typu N-classu, b=1..s.
For any N-class g from segment s of system G(n,k) there exists:
· contrast N-class g'; g+g'=nk-1.
· corresponding N-class g' v G(n+1,k) (nesting)
· corresponding N-class g' in segment s+1 (segmentation)
Instances Differences Type Nb ──────────────────────────────── 0 - - 1 3 9 2 6 N1 2 6 18 4 12 N2 4 12 10 6 2 N1 5 15 19 10 4 - 7 21 11 4 10 - 8 24 20 12 4 N2 13 - - 14 16 22 2 6 N1 17 25 23 6 2 N1 26
For number of type N-class b=1, corresponding g-number is not
divisible with nk−1.
E.g. in system G(2,4) classes g=1 a g=7 are relative prime to 15.
Number of classes in G-systems
Each segment s has N-classes with number o type b=1..s.
In G(n,k) there exists (n−b) ∙ φ(k) N-classes g(j) with number of type b.
Altogether is s∙φ(k) N-classes (i.e. k∙s∙φ(k) N-instances).
Total number N-classes v G(n,k) is:
n−1
n−1 n
∑(s∙φ(k))=φ(k) ∑(s)=φ(k) ∑(n−b)=φ(k)∙n∙(n−1)/2 N−classes
s=0
s=0 b=1
(Coefficient n(n−1)/2 reminds number of bindings of n elements).
System G(3,3) has φ(3)∙3(3−1)/2=6 natural classes (with number of type b=1 or b=2):
Number of classes in binary G-systems
There exist φ(k) N-classes g(j) in G(2,k).
(2j−1)∙g(j) mod (2k−1) =
2j−1 for nsd(j, k) = 1.
Sum of values g(j) (j=1..φ(k)) is:
∑(g) = 2k−2 ∙ φ(k)
E.g. for G(2,4) we get:
Instances Type Nb ────────────────────────── 0 − 1 2 4 8 N1 (j=1) 3 6 12 9 − 5 10 − 7 14 13 11 N1 (j=2) 15 − |
Solution: (mod 15)
j = 1: 1∙g ≡ 1 g = 1
j = 2: 3∙g ≡ 2 g = 11
|
Sum: 1+7= 8= 24−2 ∙ φ(4).
For G(2,5) it holds:
Instances Type Nb ─────────────────────────────── 0 − 1 2 4 8 16 N1 (j=1) 5 9 10 18 20 N1 (j=3) 11 13 21 22 26 N1 (j=2) 15 23 27 29 30 N1 (j=4) 31 − |
Solution: (mod 31)
j = 1: 1g ≡ 1 g = 1
j = 2: 3g ≡ 2 g = 11
j = 3: 7g ≡ 4 g = 5
j = 4: 15g ≡ 8 g = 15
|
Sum 1+11+5+15 = 32 = 25−2 ∙ φ(5).
Similarly for k = 7 (mod 127):
j= 1: 1∙g ≡ 1 g= 1 j= 4:
15∙g ≡ 8 g= 9
j= 2: 3∙g ≡ 2 g= 43 j= 5: 31∙g
≡ 16 g= 21
j= 3: 7∙g ≡ 4 g= 55 j= 6: 63∙g
≡ 32 g= 63
Sum: 1+43+55+9+21+63 = 192 = 27−2 ∙ φ(7)
Natural classes in M-systems
For natural classes (N-classes) g(j) it holds:
(nj−1)∙g(j) mod r = b∙nj−1
for nsd(j, k) = 1.
M(3,3) has all self classes natural, r = ( 33-1)/(3-1) = 26/2 = 13:
Instances Differences Type Nb
─────────────────────────────
0 - -
1 3 9 2 6 N2
2 6 5 3 1 N1
4 12 10 6 2 N2
7 8 11 1 3 N1
13 - -
M(3,4) has only 2 natural classes, r = ( 34−1)/(3−1) = 80/2 = 40:
Instances Differences Type Nb
────────────────────────────────────
0 − −
1 3 9 27 2 6 18 N2(j=1)
2 6 18 14 4 8 4 −
4 12 36 28 8 16 8 −
5 15 10 −
7 21 23 29 14 2 6 −
8 24 32 16 8 8 8 −
10 30 20 −
11 33 19 17 6 2 14 −
13 39 37 31 18 6 2 N2(j=3)
20 − −
22 26 38 34 4 8 4 −
25 35 10 −
40 − −
|
b = 1: (mod 40)
j=1: (31−1)∙ g≡ 1 no solution
j=2: (3²−1)∙ g≡ 3 no solution
j=3: (3³−1)∙ g≡ 9 no solution
b = 2: (mod 40)
j=1: (31−1)∙ g≡ 2∙1 g = 1
j=2: (3²−1)∙ g≡ 2∙3 no solution
j=3: (3³−1)∙ g≡ 2∙9 g = 13
|
In M(3,5), r = (35−1)/(3−1) = 242/2 = 121 there exists for b = 1 natural classes:
Instances Type Nb ──────────────────────────── 0 − 1 3 9 27 81 − 2 6 18 54 41 − 4 12 36 108 82 − * 5 15 45 14 42 N1(j=3) 7 21 63 68 83 − 8 24 72 95 43 − 10 30 90 28 84 − 11 33 99 55 44 − 13 39 117 109 85 − 16 48 23 69 86 − 17 51 32 96 46 − 19 57 50 29 87 − * 20 60 59 56 47 N1(j=4) 22 66 77 110 88 − 25 75 104 70 89 − 26 78 113 97 49 − 31 93 37 111 91 − 34 102 64 71 92 − 35 105 73 98 52 − 38 114 100 58 53 − 40 120 118 112 94 − * 61 62 65 74 101 N1(j=1) 67 80 119 115 103 − * 76 107 79 116 106 N1(j=2) 121 − |
b = 1: (mod 121)
j= 1: (31−1)∙ g ≡ 1 g = 61
j= 2: (3²−1)∙ g ≡ 3 g = 76
j= 3: (3³−1)∙ g ≡ 9 g = 5
j= 4: (34−1)∙ g ≡ 27 g = 20
|
Primes in R−systems
Prime-number theoremNumber of primes lesser then given number r is denoted π(r). From the first Euler’s and Legendre’s estimations follows, that value π(r) grows approximately with the same speed as function r/ln(r). Complete prove of π(r) ~ r/ln(r) did J.Hadamard and Vallée−Poussin with help of methods of complex analysis. Values π(r) are tabulated, see e.g.[Narkiewicz]:
Hadamard, Jacques| Hadamard, Jacques , 1865-1963, French mathematician, proved (y.1896) prime theorem. |
π(10²) = 25
π(10³) = 168
...
π(109) = 50847534
| Vallée-Poussin, Charles-Jean de la , 1866-1962, Belgian mathematician, proved (y.1896) - independently of Hadamard - prime theorem. |
…
...
π(1018) = 24739954287740860
π(1019) = 234057667276344607
π(1020) = 2220819602560918840
...
| Riemann, Georg Friedrich Bernhard , 1826-1866. |
Better approximation of number of primes was made by G.Riemann.
P.L.Čebyšev (y.1852) has proved so called weak-form of
prime-number theorem.
A.Selberg has proved (y.1949) prime-number theorem without
help of complex analysis.
| Dirichlet, Peter Lejeune [Dirichle], 1805-1859, |
Dirichlet has proved, that any arithmetic sequence of the 1.order (a,a+d,a+2d,...) with characteristic [d,a], (a,d)=1, contains infinite number of primes.
Primes in G-systems
We are interested if structure of G-system determines
distribution of primes. Instances of classes relative to module r
will contain all primes, that are not in prime partition of module
r.
E.g. in G(3,3) is φ(26)=12 instances relative prime to 26:
Because 26 = 2*13, must be all primes less then 26, except 2 and 13, included among 12 instances: 1, 3, 5, 6, 7, 9, 15, 17, 19, 21, 23, 25. These are: 3,5,7,17,19 and 23.
0 1 3 9 2 6 18 4 12 10 5 15 19 7 21 11 8 24 20 13 14 16 22 17 25 23 26
R(17,12,210)
0
1 17 79 83 151 47 169 143 121 167 109 173
2 34 158 166 92 94 128 76 32 124 8 136
3 51 27 39 33 141 87 9 153 81 117 99
4 68 106 122 184 188 46 152 64 38 16 62
5 85 185 205 125 25
6 102 54 78 66 72 174 18 96 162 24 198
7 119 133 161
10 170 160 200 40 50
11 187 29 73 191 97 179 103 71 157 149 13
12 204 108 156 132 144 138 36 192 114 48 186
14 28 56 112
15 45 135 195 165 75
19 113 31 107 139 53 61 197 199 23 181 137
20 130 110 190 80 100
21 147 189 63
22 164 58 146 172 194 148 206 142 104 88 26
30 90 60 180 120 150
35 175
37 209 193 131 127 59 163 41 67 89 43 101
42 84 168 126
44 118 116 82 134 178 86 202 74 208 176 52
49 203 91 77
55 95 145 155 115 65
57 129 93 111 207 159 183 171 177 69 123 201
70 140
98 196 182 154
105
210
Level: 1 2 3 4 5 6 7 8 9 10 11 12 * Total ────────────────────────────────────────────────────────────────── Classes: 3 2 0 6 0 6 0 0 0 0 0 12 * 29 Instances: 3 4 0 24 0 36 0 0 0 0 0 144 * 211
Numbers n with higher ratio n/φ(n):
n φ(n) n/φ(n) ──────────────────── 210 48 4,38 330 80 4,13 390 96 4,06 420 96 4,38 630 144 4,38 660 160 4,13 780 192 4,06 840 192 4,38 990 240 4,13 1050 240 4,38 1170 288 4,06 1260 288 4,38
Sums of powers of instance numbers
Summing in G-systems
Let us evaluate sum of numbers of instances in all classes of G(3,3):
0 0
1 3 9 13
2 6 18 26
4 12 10 26
5 15 19 39
7 21 11 39
8 24 20 52
13 13
14 16 22 52
17 25 23 65
26 26
Each sum is is divisible by number M(n,k)=(nk−1)/(n−1) = (3³−1)/(3−1) = 13.
V G(n,k), it holds for every class gi (sum through j):
∑ ui (j) = 0 ( mod M(n,k))
Computation of sum
It holds (v sum přes j):
∑ ui (j) = L(gi) ∙ c(k,q) ∙ q/k)
where q is number of transpositions (i.e. order of initial nested system), L(gi) level of class gi and c(k,q) coefficient of nesting.
E.g. v G(3,3) it holds:
L(7) ∙c(3,1) ∙ 3/3 = 3∙ ((33−1)/(3−1))∙1 = 39
L(8) ∙c(3,1) ∙ 3/3 = 4∙ ((33−1)/(3−1))∙1 = 52
...
L(13)∙c(3,1) ∙ 1/3 = 3∙ ((33−1)/(3−1))/3 = 13
g│ │ L(g) │k/q│ ∑ ui(j)
──┼──────┼───────┼───┼──────
0│ 000 │ 0 │ 3 │ 0
1│ 001 │ 1 │ 1 │ 13
2│ 002 │ 2 │ 1 │ 26
4│ 011 │ 2 │ 1 │ 26
5│ 012 │ 3 │ 1 │ 39
7│ 021 │ 3 │ 1 │ 39
8│ 022 │ 4 │ 1 │ 52
13│ 111 │ 3 │ 3 │ 13
14│ 112 │ 4 │ 1 │ 52
17│ 122 │ 5 │ 1 │ 65
26│ 222 │ 6 │ 3 │ 26
Summing in G-systems
Let us mark se sum of all e-th powers of instances in given class. We are interested in what case r | se for all e=1..k−1. Quotient se/r is denoted by small letter, i.e. se.
In case, that se is not multiple of r, we write asterisk to this place.
G(2,2) s1 G(2,3) s1 s2
──────────── ───────────────────────
0 0
1 2 1 1 2 4 1 3
3 3 6 5 2 10
7
G(2,4) s1 s2 s3
─────────────────────────────────
0
1 2 4 8 1 * 39
3 6 12 9 2 18 180
5 10 1 * 75
7 14 13 11 3 * 441
15
G(2,5) s1 s2 s3 s4
───────────────────────────────────────
0
1 2 4 8 16 1 11 151 2255
3 6 12 24 17 2 34 668 14110
5 10 20 9 18 2 30 506 9102
7 14 28 25 19 3 65 1533 37949
11 22 13 26 21 3 61 1323 29965
15 30 29 27 23 4 104 2794 76748
31
Summing in R-systems
We are interested, in what case all sums s1,s2,...,sk−1 are divisible by number r. The following systems have this property.
Let us separate systems according to Mersenne’s (M) or Fermat’s (F) systems.
M-systems:
R(2,2,3), R(2,3,7),
R(2,5,31), R(2,7,127), R(3,3,13),
R(3,5,121), R(4,2,5), R(4,5,341),
R(5,3,31), R(5,5,781),
R(6,2,7), R(6,3,43), R(7,5,2801),
R(8,2,9), R(8,3,73), R(8,5,4681),
R(9,3,91), R(10,2,11), R(11,3,133), R(12,2,13),
R(12,3,157),
F-Systems:
R(2,2,3),R(2,4,17)
All mentioned systems have prime order k or prime module r.
But only systems with prime module r does not have this property, see e.g. M-system R(9,3,91), where r = 91 = 7∙13:
R(9,3,91) s1 s2
────────────────────────────────────
0
1 9 81 1 73
2 18 71 1 59
3 27 61 1 49
4 36 51 1 43
5 45 41 1 41
6 54 31 1 43
7 63 21 1 49
8 72 11 1 59
10 90 82 2 164
Sums in R-systems of order 3
We are interested, for what systems of order 3 there exists sums of powers 1.a 2. degree (as e.g. v G(2,3)=R(2,3,7), M(3,3)=R(3,3,13),...). For class g we get:
Degree Sum
───────────────────────────────────────────────────────
1. g + gn + gn2 = g(1+n+n²) = g (n³−1)/(n−1)
2. (g)² +(gn)²+(gn²)² = g²(1+n²+n4) = g(n6−1)/(n²−1)
Sums of 1.degree are divisible by r:
- In G-systems G(n,3)=R(n,3,r), r=n³−1, if n = 2 (i.e.n−1=1).
- In all M-systems M(n,3)=R(n,3,r), r=(n³−1)/(n−1).
Sums of 2.degree are divisible by r:
- In G-systems G(n,3)=R(n,3,r), r=n³−1, if (n6−1)/(n²−1)/(n³−1) ε N, i.e. if (n−1) | (n²−n+1), what is possible in case n=2 only.
- In all M-systems M(n,3)=R(n,3,r), r=(n³−1)/(n−1), because ((n6−1)/(n²−1))/((n³−1)/(n−1))= (n³+1)/(n+1)=(n²−n+1) ε N.