Solar activity - Resonance

You're reading an English translation of the original Czech page.

A.M.Molchanov

A.M.Molchanov, Russian mathematician. He devoted himself to mathematical modeling in biology, ecology, genetics, etc. He assumed resonance structure of the solar system. The development of the planet's leads to resonances and orbital periods in the ratio of small integers. He suggested some relationships for both the sun and the sun system, as well as for the systems of Jupiter and Saturn.

Resonance of orbital periods

Introduction

Three Jupiter and three Uranus moons respect the so-called Laplace resonance, which limits the possibility of multiple conjunctions. It is a certain principle of minimal interaction - which ensures balance.

Therefore, resonance does not generally only represent a disturbing element (which can break objects, destroy bridges, etc.), but it can also be a thing to ensure synchronization and stability.

There is a simple argument regarding the moon of Jupiter / Uranus: they are synchronized thanks to the tidal forces. According to A.M.Molchanov (1965, 1968), however, the bodies can be synchronized even when operating by very weak forces. Molchanov considers "small dissipative forces", in some newer theories also other hypotheses were proposed (M. B. Gubaidullin, 2015, see also N. Scafetta, 2013).

According to the behavior of Jupiter / Uranus moons, generalization offers: multiple conjunctions of bodies are not desirable in the Solar System - there is a tendency for them to appear only minimally, not to appear exactly or to be somehow balanced.

Small (tidal) effects can enhance the natural oscillation of the solar atmosphere and cause great changes.

Resonances of the inner planets

J.J.Condon and R.R.Schmidt at work (1975) derive a resonance relationship in the form Lt = 3 * Lv -5 * Le + 2 * Lj where Lv, Le and Lj are the longitude of Venus, Earth and Jupiter.

From the comparison of the synodic periods of the planets, ((E, J) / 5, (V, J) / 3) = 2 · W. Then 1 / (2W) = 3 / V-5 / E + 2 / J, and 2W = 22.13505 years, ie, W = 11.06753 years .
Maximum solar activity occurs approximately when (for the longitude of Venus, Earth and Jupiter):

3L_V - 5L_E + 2L_J = kπ

But that does not always apply ...

Wilson's refinement

Here we derive:

41L_V - 69L_E + 28L_J = kπ

A period of 22,386 years is based on 41/69 (K.Takahashi, 1967).

Maya

For 2W = 22.3855 years, Jupiter will go back by 40.6 dg, ie, if we observe the system with a 2W period, we will sense that Jupiter is orbiting the period with the period about 198.4 years. If he really moved, he would meet Saturn every 25.65 years, ie 4 * I or 3 * Y, where I is the period of the inner planets = 6.4 years and Y is 8.54 years. The difference between 25.65 and 22.39 years is 3.26 years. (52 Tun / 72 Almanac Cycle 18720 d, Calendar Round 52 Haab / 73 Almanac Cycle 18980 d).

Molchanov's Resonances

Molchanov's Resonance: [M, -V, -E / 2, -R] [V, -R / 3, -S] [E, -R, 2, J, / 2] [U, -U / 7], [U, -N / 2], [U, -P / 3] (plus their linear combination ...)

Resonance with period H

In the repetition of the climatic periods, there is a so-called Hallstatt cycle (H = 2300 years) which correlates with the resonance of orbital periods of outer planets.

The difference of 2403.05 years and 2224.10 years (with the sum of 4627 years) is 178.95 years, but the common divisor is the period 185.1 years (+ -0.2 years) which can be modeled by resonance 1 / J-3 / S + 2 / N (or ((U, N), H)).

Balancing of Jupiter

Influence of Neptune

Line of conjunctions V-E-J move (backward) with period: P= (W,J) = (11.06753, 11.861983) = 165.25 years, i.e. approximately with orbital period of Neptune.
Axial period Jupiter-Neptun [J,N] = 22.13075 y = 2*11.06538 years coincides with period of Solar activity.
Some authors (Ray Tomes,…) connect solar period with these two bodies ( Jupiter, Neptune).
(In combination with resonance of inner planet it leads to 6/V-10/E+3/J-1/N = 0, i.e. unstable resonance).

Importance of Jupiter (with a view to the weight) is clear. Neptune might acquire its influence by the distance from the sun, see, for example value (M * R2 (moment of inertia):

	M [10²⁴ kg]	a [10⁹ m]	Ma2 [10³⁹kgm²]
Jupiter	1899,0	778,6	1151,2
Saturn	568,0	1433,5	1167,2
Uran	86,8	2872,5	716,2
Neptun	102,0	4495,1	2061,0.

Resonance

Also period of resonance 1/W = 1/J + 1/U – 1/N correlates by value W = 11.094 years with the mean period of the Solar cycle. Let us write it to form of stable resonance: 1/W - 1/J + 1/N - 1/U = 0.

Resonance maxima occur, when it holds (for longitudes of Jupiter, Jupiter perihelion, Uranus and Neptune):

Lj – Ljp + Lu - Ln = π+2kπ

Resonance minima occur, when it holds (for longitudes of Jupiter, Jupiter perihelion, Uranus and Neptune):

Lj – Ljp + Lu - Ln = 2kπ

This resonance binds the period of solar activity W with orbital periods of planets Jupiter, Neptune, Uranus. Saturn's here seemingly outside game - however it is bound by resonance of outer planets to Jupiter perihelion (viz Influence of Jupiter)!?

Depiction of the relationship

The resonance arise as a sum of the two delta angles ∆J + ∆UN where:

∆J = Lj-Ljp (Jupiter with regard to its perihelion)
∆UN = Lu-Ln (Uranus with regard to Neptune).

n	M_o	∆J	∆UN	n	M_o	∆J	∆UN	n	M_o	∆J	∆UN	n	M_o	∆J	∆UN
-30	1416,7	316	224	-14	1594,4	306	234	2	1772,0	296	244	18	1949,5	283	257
-29	1428,0	296	244	-13	1605,6	286	254	3	1783,1	273	267	19	1960,5	257	283
-28	1439,2	275	265	-12	1616,6	262	278	4	1794,1	246	294	20	1971,4	229	311
-27	1450,2	251	289	-11	1627,6	235	305	5	1805,0	218	322	21	1982,4	203	337
-26	1461,2	224	316	-10	1638,5	207	333	6	1815,9	192	348	22	1993,4	180	0
-25	1472,0	197	343	-9	1649,4	182	358	7	1826,9	168	312	23	2004,5	159	21
-24	1483,0	172	8	-8	1660,5	160	20	8	1838,1	149	31	24	2015,7	140	40
-23	1494,1	150	30	-7	1671,6	140	40	9	1849,3	130	50	25	2026,8	120	60
-22	1505,3	130	50	-6	1682,8	120	60	10	1860,4	109	71	26	2037,9	96	84
-21	1516,4	110	70	-5	1694,0	99	81	11	1871,5	85	95	27	2049,0	70	110
-20	1527,5	88	92	-4	1705,0	74	106	12	1882,5	58	122	28	2060,0	42	137
-19	1538,6	63	117	-3	1716,0	47	133	13	1893,5	31	149	29	2071,1	18	162
-18	1549,6	36	144	-2	1727,1	21	159	14	1904,6	7	173	30	2082,3	356	184
-17	1560,7	10	170	-1	1738,2	357	183	15	1915,9	346	194	31	2093,6	336	204
-16	1571,9	346	194	0	1749,5	336	204	16	1927,2	326	213	32	2104,8	316	224
-15	1583,7	326	214	1	1760,8	316	224	17	1938,4	306	234	33	2116	294	246

Simplified diagram of solar activity power follows.
Observed maximum so (according to axes direction) can be of 4 distinct types,
see e.g. I.1727.5 (140.0), II.1870.6 (140.5), III. 1989.6 (150.1), IV. 1957.9 (201.3) :

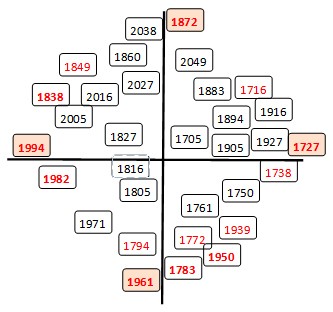
Maxima of Solar activity

Comparison of extremes

In the following overview these maxima are compared:

maximum of Solar activity M_S
maximum of Wood's resonance of inner planets M_I: 3L_V - 5L_E + 2L_J = kπ
maximum of resonance of balancing the outer planets M_O: L_J - L_N + L_U = L_JP + π (+2kπ)
maximum of resonance of geometrical axes M_A: (L_J - L_S) + (L_N - L_U) = kπ/2

1500-1650

N	W_S	W_I	W_O	W_A	W_I-W_S	W_o-W_S	W_o-W_I
-23	1492	1494,6	1494,1	1490,4	2,6	2,1	-0,5
-22	1505	1505,8	1505,2	1501,6	0,8	0,2	-0,6
-21	1519,0	1517,3	1516,4	1513,1	-1,7	-2,6	-0,9
-20	1528,0	1527,5	1527,5	1523,7	-0,5	-0,5	0,0
-19	1539,0	1539,1	1538,6	1535,6	0,1	-0,4	-0,5
-18	1548,0	1549,6	1549,6	1546,9	1,6	1,6	0,0	P-maximum
-17	1558,0	1560,8	1560,7	1558,1	2,8	2,7	-0,1
-16	1572,0	1572,5	1571,9	1570,1	0,5	-0,1	-0,6
-15	1581,0	1583,6	1583,7	1580,4	2,6	2,7	0,1
-14	1591,0	1594,6	1594,4	1591,7	3,6	3,4	-0,2
-13	1604,0	1606,2	1605,6	1602,8	2,2	1,6	-0,6	1607 - Kepler's spot
-12	1615,5	1616,8	1613,1	1613,0	1,3	1,1	-0,2	1618 - Simon Mair's (Marius) spots
-11	1626,0	1627,8	1627,6	1625,3	1,8	1,6	-0,2
-10	1639,5	1638,8	1638,5	1636,3	-0,7	-1,0	-0,3

1650-1800

n	W_S	W_I	W_O	W_A	W_I-W_S	W_O-W_S	W_O-W_I
-9	1649,0	1649,9	1649,4	1647,5	0,9	0,4	-0,5
-8	1660,0	1660,8	1660,5	1659,2	0,8	0,5	-0,3	1660 - Hevelius spots, 1661 - Boyle and Picard sunspot group
-7	1675,0	1672,2	1671,6	1669,5	-2,8	-3,4	-0,6	1671 (August) - Pickard spot, Hevelius spot, 1676 - Pickard extreme, Maunder
-6	1685,0	1682,5	1682,8	1681,0	-2,5	-2,2	0,3	1684 - Pickard extreme, Cassini, Kirch
-5	1693,0	1693,5	1694,0	1692,2	0,5	1,0	0,5
-4	1705,5	1705,2	1705,0	1703,1	-0,3	-0,5	-0,2
-3	1718,2	1716,0	1716,0	1715,2	-2,2	-2,2	0,0	1716 - visible aurora, 1714-15 - P-maximum, end of Maunder period
-2	1727,5	1727,4	1727,1	1726,3	-0,1	-0,4	-0,3
-1	1738,7	1738,5	1738,2	1737,8	-0,2	-0,5	-0,3
0	1750,3	1750,1	1749,5	1749,2	-0,2	-0,8	-0,6	1752 - second maximum
1	1761,5	1761,3	1760,8	1759,7	-0,2	-0,7	-0,5
2	1769,7	1771,8	1772,0	1771,4	2,1	2,3	0,2	1774 - second maximum
3	1778,4	1782,8	1783,1	1782,3	4,4	4,7	0,3
4	1788,1	1794,5	1794,1	1793,4	6,4	6,0	-0,4

1800-1950

n	W_S	W_I	W_O	W_A	W_I-W_S	W_O-W_S	W_o-W_I
5	1805,2	1805,5	1805,0	1805,7	0,3	-0,2	-0,5
6	1816,4	1815,6	1815,9	1816,3	-0,8	-0,5	0,3
7	1829,9	1827,2	1826,9	1827,7	-2,7	-3,0	-0,3
8	1837,2	1838,3	1838,1	1838,7	1,1	0,9	-0,2
9	1848,1	1849,2	1849,3	1848,9	1,1	1,2	0,1	1847-48 - Giant sunspots
10	1860,1	1860,2	1860,4	1860,7	0,1	0,3	0,2	1859 - proton event (Carrington), 1864 - second maximum, 1859-60 - Giant sunspots
11	1870,6	1871,3	1871,5	1871,6	0,7	0,9	0,2	1870-71 - Giant sunspots, 1870 - proton event (Young)
12	1883,9	1881,7	1882,5	1882,9	-2,2	-1,6	-0,8	1882 - P-maximum, 1882 - Giant sunspot, 1882 - proton events (Maunder)
13	1894,1	1893,5	1893,5	1894,9	-0,6	-0,6	0,0	1892-93 - Giant sunspots, 1892 - proton events (Rudeaux)
14	1907,0	1904,5	1904,7	1905,7	-2,5	-2,3	-0,2	1905,07,08 - Giant sunspots, 1908 - proton event
15	1917,6	1916,1	1915,9	1917,3	-1,5	-1,7	-0,2	1917 - Giant sunspot, 1917 - proton event
16	1928,4	1926,7	1927,2	1928,4	-1,7	-1,2	-0,5	1926,29 - Giant sunspots, 1926 - proton event
17	1937,4	1937,9	1938,4	1939,1	0,5	1,0	0,5	1935,37-42 - Giant sunspots, 1938 - proton event
18	1947,5	1949,5	1949,6	1951,1	2,0	2,1	0,1	1946 - proton event, 1949 - proton event

1950-2100

n	W_S	W_I	W_O	W_A	W_I-W_S	W_O-W_S	W_O-W_I
19	1957,9	1960,5	1960,5	1962,1	2,6	2,6	0,0	1958 - the highest level since Galileo's observations (1610), 1956,59-61 - proton events
20	1968,9	1972,2	1971,4	1973,8	3,3	2,5	-0,8	1969 - proton event, 1972 - extreme flare, 1972 - second maximum
21	1979,9	1983,2	1982,4	1985,5	3,3	2,5	-0,8	1981 - extreme flare
22	1989,6	1993,2	1993,4	1996,1	3,6	3,8	0,2	1990 - the second highest level since Galileo's observations (1610)
23	2000,5	2004,3	2004,6	2007,8	3,8	4,1	0,3
24	?	2015,3	2015,7	2018,3	?	?	0,4
25	?	2026,1	2026,8	2028,9	?	?	0,7
26	?	2036,6	2037,9	2040,9	?	?	1,3
27	?	2048,1	2049,0	2051,5	?	?	0,9	2050-51 - P-maximum
28	?	2059,5	2060,0	2063,4	?	?	0,5
29	?	2070,6	2071,1	2074,7	?	?	0,5

Subsequent considerations

Regularities

Theoretical extremes (maxima as well as minima) of solar activity take place about with the same period as the actual extremes. The biggest differences in maximum are observed in years 1583-1606, 1675-1685, 1778- 1788, 1829, 1958-2000. The biggest differences in minimum are observed in years 1553,1619, 1784, 1902-1924,1996.

Justin Flynn has noticed certain regularities of these deviations (personal communication).

Consider the following chart:

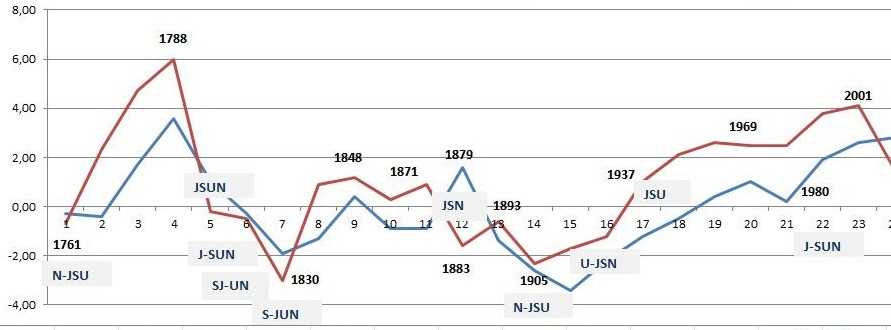
Rule of alternating deviations

Let us divide the Uranus-Neptune conjuction cycle to following time-periods, and to write departures taken from the column Mo-MS of the tables above:

    Time-      Departures
    period     sign  maxima   minima
    ------------------------------------
    1543-1586  -
    1586-1628  +
    1628-1671  -
    1671-1714  +
    1714-1757  -  1718-1761  1745-1765
    1757-1800  +  1769-1788  1777-1799
    1800-1842  -  1805-1830  1810-1832
    1842-1885  +  1838-1871  1844
    1885-1928  -  1884-1928  1856-1943
    1928-1971  +  1938-2004  1954-2008
    1971-2014  -  ?????????
    2014-2057  +

For the period 1714 -1971 all seems to work quite well. But this rule (like the rule from the paragraph Coincidence of geometrical axes) fails - and again roughly after year 1960!?)

Correction of extremes W_O

Let dUN = Neptune.Longitude - Uranus.Longitude, dJJa = Jupiter.Longitude - Jupiter.LongPerihelion - 180 and we look for extremes where dUN + correction = dJJa (with a given precission, e.g. 5 dg).

The following function was derived from the previous paragraph: f = Cos(2*dUN) * abs(Cos(2*dUN)) = sign(Cos(2*dUN)) * Cos²(2*dUN) with a correction angle equal to k * f. For value of the constant k = 120 we get the following table:

Table of corrected extremes

    Diff    Theory     Jp    J    S    U    N  f(dUN)  Corrected   Observation
 ------------------------------------------------------------------------------
    11,28   1749,39 -  15  346  231  322  118  +0.38   1750,73     1750.3  *
1757
    11,25   1760,65 -  14  326  358    6  143   0.00   1760,72     1761.5  *
    11,20   1771,84 +  14  305  146   51  167  -0.30   1770,79     1769.7  *
    11,09   1782,93 +  13  281  276   98  191  -0.87   1779,56     1778.4  *
    11,01   1793,94 +  14  256   46  148  215  -0.70   1791,19     1788.1  ?
1800
    10,92   1804,86 -  15  229  191  200  238  +0.06   1805,13     1805.2  *
    10,92   1815,79 -  15  203  314  249  262  +0.98   1819,56     1816.4  ?
    11,01   1826,79 -  14  179   92  296  286  +0.73   1829.80     1829.9  *
    11,14   1837,94 +  14  159  233  340  310  +0.21   1838,80 	   1837.2  . 
1842
    11,17   1849,11 +  14  140  359   24  334  -0.02   1849,04     1848.1  *
    11,17   1860,28 +  14  119  147   69  359  -0.48   1858,55     1860,1  *
    11,12   1871,39 +  15   97  277  118   24  -0.99   1868,05     1870,6  ?
    10,98   1882,37 -  15   69   48  169   48  -0.29   1881,41     1883,9  ?
1885
    11,01   1893,38 -  14   41  193  220   72  +0.25   1894,28     1894,1  *
    11,14   1904,52 -  14   17  318  270   97  +1.00   1908,13     1907,0  *
    11,23   1915,75 -  14  356  101  315  122  +0.66   1918,04 	   1917,6  *
    11,34   1927,08 -  16  338  242  360  147  +0.14   1927,54     1928,4  *
1928
    11,23   1938,31 +  16  317   10   44  171  -0.08   1938,11     1937,4  *
    11,12   1949,42 +  14  294  157   91  195  -0.63   1947,03 	   1947,5  *
    10,98   1960,40 +  14  267  284  141  218  -0.99   1956,54     1957,9  *
    10,90   1971,30 +  14  239   55  192  242  -0.03   1971,21     1968,9  ?
1971
    10,95   1982,25 +  15  214  199  242  265  +0.68   1984,90     1979,9  ??
    11,03   1993,29 +  16  191  323  289  289  +0.94   1997,03     1989,6  ??
    11,12   2004,40 +  15  170  105  334  313  +0.47   2006,28 	   2000,5  ??
    11,14   2015,55    14  150  243   17  338  +0.78   2015,70             ?
2014

Rows with "acceptable" results are marked by asterisks.

Other resonances

Listing

Resonances observed above are not only resonances producing cycles with period close to the period of solar activity. For example (J/1,-S/2,+U/4,-N/3) = 21.8 years while (J/1,-S/3,+U/4,-N/2) = 55.8 years. Also (S/1,+U/3,-N/4) = 22.0 years, therefore e.g. cos(Ls+3*Lu-4*Ln) oscillates with 11-years period etc.

    J  S  U  N        k*W          M 
    ------------------------------------
    0  3  1 -4        11,2       -971,5
    1  0  2 -3        11,1      -1671,2
    2 -3  3 -2        11,1      -5971,4
    0  1  3 -4        22,0       7807,8
    1 -1 -1  1        22,5      -1376,5
    0  1 -1  0        45,4      -1724,2
    1 -2  0  1        44,5      -6717,5
    0  0  2 -2        85,7       2829,8
    0  1 -3  2        96,3      -1072,9
    1 -3  3 -1        82,7       1275,0

Resonance with inclusion of Saturn

Now let us consider resonance with period 44.5 years according to row:

 J  S  U  N        k*W          M 
 ------------------------------------
 1 -2  0  1        44,5      -6717,5

After rewriting to the form:

L_J - 2* L_S + L_N = L_JP + k*π/2

we get new values W_N (we will compare them to extremes W_O):

Spacing     W_N     W_O
   0,00   1605,503	1605,6
   9,09   1614,593	1613,1
  14,84   1629,433	1627,6
   8,27   1637,701	1638,5
  10,82   1648,516	1649,4
  13,03   1661,548	1660,5
   8,10   1669,652	1671,6
  14,26   1683,917	1682,8
   9,67   1693,582	1694,0
   9,75   1703,329	1705,0
  13,61   1716,936	1716,0
   9,42   1726,355	1727,1
  11,80   1738,155	1738,2
  12,21   1750,366	1749,5
   9,34   1759,702	1760,8
  13,53   1773,228	1772,0
   9,91   1783,139	1783,1

Spacing   W_N     W_O
   9,75   1792,886	1794,1
  14,35   1807,232	1805,0
   8,19   1815,419	1815,9
  12,70   1828,123	1826,9
  11,14   1839,266	1838,1
   8,27   1847,534	1849,3
  14,59   1862,127	1860,4
   9,25   1871,382	1871,5
    
  10,16   1881,539	1882,5
  13,28   1894,818	1893,5
   9,34   1904,154	1904,7
  12,54   1916,694	1915,9
  11,47   1928,166	1927,2
   9,75   1937,913	1938,4
  13,61   1951,520	1949,6
   9,58   1961,103	1960,5

   
Spacing   W_N     W_O
  10,98   1972,082	1971,4
  13,11   1985,196	1982,4
   8,27   1993,465	1993,4
  14,10   2007,565	2004,6
  
   9,58   2017,148	2015,7
   8,52   2025,663	2026,8
  14,76   2040,420	2037,9
   8,76   2049,181	2049,0

Good agreement between the extremes W_N and W_O exists due to resonance [J/3, -S/8, -U, N/5] (it is derived from the difference of the terms for W_N and W_O as a function of planetary longitudes...). Leading period of this resonance is (J/3, S/8) = 53.555 years (ie. B/8, divisor of Babylonian period B).
But - whether all the periods have to be measured relative to Jupiter's perihelion, or to other points (e.g. each planet to its perihelion etc.) - is not clear.
The values of the spacing (i.e. the distance of two neighboring extremes) appear to be bi-modal, similar to the real solar cycles. But do not correspond to the observed intervals.

Other observations

Significant deviation

Interval of years 1761 - 1805 (with a centre around y. 1783) may be important. There would be solar-activity extremes expected on years marked by # (odd rows), but real activity was observed rather on years marked by asterisks:

Theory      Jp    J    S    U    N    Observation
-------------------------------------------------------
# 1760,65 ***  14  326  358    6  143    1761.5 
1765,96      14  136   66   27  154    
# 1771,85 ***  14  305  146   51  167    1769.7
1777,08 ***  13  115  211   73  179    1778.4
# 1782,94      13  281  276   98  191   
1788,14 ***  13   90  334  122  202    1788.1
# 1793,94      14  256   46  148  215  
1799,14      14   63  117  173  226  
# 1804,87 ***  15  229  191  200  238    1805.2

There is certain symmetry or perpendicularity, alignment of outer planets on the year. 1783 (see image of planetary position - Jupiter perihelion is on the right side of the image...!?)