Babylonian period
Introduction
The Babylonian period is a significant period of movement of the inner planets. Makes approximately B=427 years.
References
Ray Tomes
Ray Tomes included the Babylonian period in his schemes (see Theoretical cycle periods):
427.0 213.5 106.8 53.38 26.69
142.3 71.17 35.59 17.79 8.897 4.448 2.224
Timo Niroma
1. 415-425 years
2. 305-314 years
3. 260-280 years, affects moisture
4. 177-227 years, almost all, very pronounced,
an intensity cycle, affects temperature
(median 202 years)
5. 154-157 years, a length cycle, 13 Jovian years
6. 143-148 years, a length cycle, 13 average cycles
7. 104-105 years, half of the 200-year cycle
8. 85- 90 years
9. 78- 79 years, the Gleissberg cycle
10. 63- 67 years, 1834-1901, (1954-?)
11. 57- 59 years
12. 51- 52 years, 1783-1834, 1901-1954
13. 43- 45 years
Natural phenomena
Storm at Sea
On November 11, 1099, floods hit the coasts of England, Belgium and Holland (see e.g. Encyclopaedia Britannica) Flooding occurred in the Thames Estuary, with the flood "rising to such a height and doing so much damage, as no one remembered..." (Lowe, 1870). Estimated to have perished in coastal flooding up to around 100,000 people (Taylor Redd, 2012; Haigh and Bradshaw, 2015).
On January 31, 1953, England, Belgium, Holland and Scotland were hit by a great flood in the North Sea (associated with a storm surge). The flood was assessed as the worst flood England and Scotland in the 20th century, several thousand people and tens of thousands of animals lost their lives and tens of thousands of people had to leave their homes. The flood became a model for the Dutch the disaster film "The storm" (2009).
The distance between these two floods is 1953-1099 = 854 years = 2 * 427 years. The period of 427 years was already known to the Babylonians. It made it possible to approximate 36 sidereals period of Jupiter (36*11.862 years = 427.03 years) using its 391 synodic periods (i.e. the period of eclipses of the Sun-Earth-Jupiter, 391*398.884 days = 427.00 years).
He offers to search for what happened on Earth in the year 1526 (= 1099+427 years). And indeed: the medieval fishing village of Skegness on the coast North Sea (now a seaside resort in the English county of Lincolnshire) destroyed by a storm in 1525-26. It may also be interesting that in the vicinity of the year 1526, the "world flood" was predicted - according to the conjunction of the planets - for the year 1524.
The agreement is striking, the coast of the North Sea may be accordingly threatened again - in the vicinity of the year 2380 (= 1953+427 years).
We summarize the result in the following table:
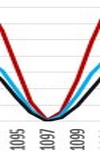
Holland y.1099 England, Belgium |

Skegness y.1526 England |
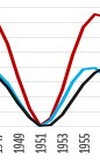
Holland y.1953 England, Belgium |

Year 2380 (prediction) North Sea |
Eruption of Mount Vesuvius
In a series of years 79, 506, 933, 1360, 1787, 2214, 2641 ... with an interval of 427 years below we find three eruptions of the volcano Vesuvius, of which the most famous and the most tragic is the first of them, from 1979:
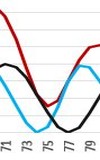
Vesuvius y.79 (destroyed Pompeii) |
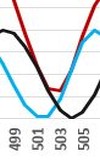
Vesuvius y.505 |
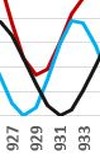
Vesuvius y.933 |

1360? |
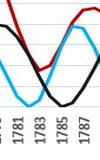
Vesuvius y.1787 |

Year 2214 (prediction) |
Planetary motion
Outer planets
Let us assume two relations:
- synchronization of axes of outer planets with Jupiter
([J,U],[S,N]) = 3∙J
- synchronization of axes of outer planets with solar cycle
([J,N],[S,U]) = 4∙W
From equations (1/J+1/U)-(1/S+1/N) = 1/(3J) and (1/J+1/N)-(1/S+1/U) = 1/(4W) it follows W= 3/4(J/2,S/3)= 11.23375 years = [J,212.1 years].
And hence:
W= 3/4(J/2,S/3)= [J,B/2]
(But in comparison with the mean period of Solar cycle Ŵ=11.0-11.1 years is value 11.23 years too high).
Derived periods
Period 71 years
Babylonian counted also with the cycle B/6 = 6*J = 71.17 years (see Earthquakes).
65 oscillatory years give c. 71 years, i.e. 6 orbital period Jupitera.
1.091854 years: 9/2*(E,R/2)/65 = 9/2*(0.999979,1.880711/2)/65 = 70.97052/65 = 9/2*15.7712270/65
- 70 years: geological cycle (mud of Lake Saks)
- 70 years: cycle from tree rings (Japanese cedar tree)
- 70.9856 years: 65 oscillation years, 65*(E,J)=65*1.0920855 (tropical)
- 71.1391 years: 6*J (tropical), 71.1769 years: 6*J (anomalistic) =100 tzolkin
- 71.1785 years: B/6 = 427.07 years/6
- 71.1861 years: 4627.1/65 (925.4/13)
- 71.74 years: 2*(S,N) =2*35.87 years
- 73 years: geological cycle (banded clays)
Extrapolation of low solar activity from 1800-1830 to 1980-2010 went wrong, 180 years cycle failed. But in this case also 320 years cycle go wrong, because of Maunder’s minimum in years 1660-1690.
Schove, Derek Justin| Schove, Derek Justin , (1913-1986) English meteorologist and astronomer engaged in dating historical events in relation to natural phenomena (eclipses, auroras, floods, storms, etc.). Author of many papers, articles and books. Reconstructed retrospectively values of solar activity. |
In Schove’s dates periods of high (SSS,SS,S) and low (WW,W) solar activity seems to change with period more than 180 years. E.g. progress with step 205 years (about half of Babylonian period) we get e.g. years: 350, 555, 760, 965, 1170, 1375, 1580, 1785, 1990. Nearby (±40 years) of these dates relatively high maxima appear. (Tidal action of planet J-V-E cannot make such differences…!?)
Period 284 years
Simulation of motion of inner planets (with Bretagnon’s data) establishes especially part 2/3 of Babylonian period, i.e. period c. 284 years
Period 1025 years
I have noted the possibility of phase shifts of conjunction cycles while reading texts (paragraph about period 1020-1030 years) of climatologist Timo Niroma:
More notable extremes of solar activity seems to appear every c. 1025 years, i.e. 6*(U,N), 12B/5:
"The auroral data of G. L. Siscoe of the years 450-1700 (Rev. Geophysics and Space Physics 18, 1980) give another chance to try to calculate a value for the 1000-year cycle. The lowest superminimum (smoothed) between 450 and 1450 appeared from 620 to 680. It precedes the lowest superminimum of this millennium, the Maunder Minimum in 1640-1700 by 1020 years. The next superminimum after this pre-Maunder is in 780-800, which apparently corresponds to the superminimum in 1800-1820 both by duration and relative height with a 1020 year delay. The third superminimum in the Siscoe data is in 850-880 corresponding to the superminimum in 1880-1920 about 1030 years later. The Siscoe supermaxima in 740-770, 820-850, and 900-930 correspond to supermaxima beginning 1030, 1010, and 1050 years later, so that a supercycle of 1020-1030 years in average length is rather apparent." ( Timo Niroma, "Sunspots: Sunspot cycles and supercycles and their tentative causes")
Period G.L.Siscoe 1025 years: 5125/5;
minima v Eddyho diagramu Solar activity (-9625,-8600,-7575,-6550,-5525,-4500,-3475, -2450,-1425, -400, +625, 1650, 2675, 3700)
Data in the following table progress in the rough with Babylonian period 427 years. On the left are instants of conjunctions E-Ln-R and instants of Jupiter in perihelion.
E-Ln-R Jp U-N --------------------------------- -2021.55 -2022.63 -1594.48 -1595.57 * (-1605.74) -1167.41 -1168.50 -740.34 -741.44 * ( -745.20) -313.26 -314.37 113.81 112.69 * ( 111.19) 540.88 539.76 967.94 966.83 * ( 965.47) 1395.01 1393.90 1822.08 1820.97 * ( 1821.01) 2249.15 2248.04 2676.22 2675.11 * ...
Possible correlations with conjunctions Uranus-Neptune are marked on the right.
If mean period (U,N) was 170.813 years, then it would be equal to 20* Y= 80* (E,R)= 240 z. It would have integer ratio to Babylonian period (2:5), to 1025 years period of polar lights G.L.Siscoe (1:6) and also to Mayan period M=5125 years (1:30).
The following data (with period M/5 = 5125/5 = 1025 y)
seams to appear near to minima on Eddy diagram of solar
activity:
-9625,-8600,-7575,-6550,-5525,-4500,-3475, -2450,-1425, -400,
625, 1650, (2675), (3700).
These data (with period M/3 = 5125/3 = 1708 y) remind
great eruptions of volcanoes:
-5049 ?, -3341 Avelino, -1633 Thera, 75 Vesuvius, 1783 Laki, 3491 ?.
Účinek Uranu s Neptunem
Všechna tři uvedená data bouří na moři se kryjí s okamžiky kvadratur planet Uran-Neptun. Poloha planet 31.1.1953:
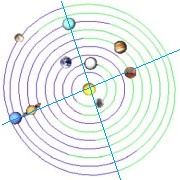
Babylónská perioda tvoří totiž poměrně přesně 2.5 násobek synodické periody Uran-Neptun: 427 let = 2.5 * 170.8 let.
Také erupce v okolí roku 1787 (tj.výbuch Etny y.1787, Stromboli 1783, Laki y.1783-84) nastaly poblíž kvadratury planet Uran-Neptun. Poloha planet 1.7.1787:
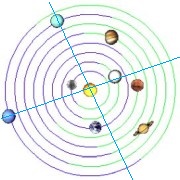
Great inequality
Great inequality (J/2,S/5) makes c. 2*B=72*J=29*S=400*(E,R).
Let us assume I= 2∙B = 72∙J = 29∙S' = 43∙(J,S').
Then using J=11.8620 we get: I=854.06 years, B=427.03 years, S' =
29.450441 years. Synodic period (J,S') = 19.861925 years.
If value of great inequality J-S was just value I= 2*B=
854.06 years, then derived periods differ from the Bretagnon’s
periods by ratio:
S/S'=29.457158/29.450441 = 1.000228;
(J,S')/(J,S)=19.861925/19.8588709= 1.000154.
Laplace's cycle
7*61 let = 427 let, odtud 854 let vs.Laplaceův cyklus. Datování:
... 59, 273 - 486, 700, 913, 1127 - 1340, 1554, 1767, 1981 - 2194, 2408, 2621,...
- y.1340 uprostřed období zesílení (vysoká aktivita)-střední rychlost Jupitera,
- y.1553-1554 je uprostřed přechodného období (nízká aktivita) - vyšší rychlost Jupitera,
- y.1760 - střední rychlost Jupitera,
- y.1981 je uprostřed přechodného období (nízká aktivita) - nižší rychlost Jupitera,
Overlapping of cycles
Separation of conjunctions
Synodic period is mean period of repetition of conjunctions. In reality conjunctions occur (in consequence of elliptical orbits and non-uniform motion of bodies) in irregular intervals.
E.g. conjunctions J-S, in years 1940-2000: 1940.85, (20.41), 1961.26, (20.01), 1981.28, (19.15) and 2000.43 (in parenthesis are intervals):.
Conjunctions J-S
Intervals of conjunctions Jupiter-Saturn repeats in triads, i.e. with mean period c. 60 years (Chinese astrological cycle), 3*(J,S) = 3*19.859 y = 59.577 y.
In every 900 years (great inequality) phase shift appears and new sequence of triads begins.
E.g. maximum separation c. 20.5 years appears before conjunctions in years 750.03, 1723.11 and 2636.65.
I. y. 750.03
0: ( 20.49) 750.03 ( 19.59) 769.62 ( 19.47) 789.08
1: ( 20.48) 809.56 ( 19.69) 829.25 ( 19.38) 848.63
2: ( 20.48) 869.11 ( 19.77) 888.88 ( 19.32) 908.20
3: ( 20.45) 928.65 ( 19.86) 948.51 ( 19.25) 967.76
4: ( 20.42) 988.18 ( 19.96) 1008.14 ( 19.19) 1027.34
5: ( 20.38) 1047.72 ( 20.04) 1067.76 ( 19.15) 1086.91
6: ( 20.34) 1107.26 ( 20.11) 1127.37 ( 19.14) 1146.50
7: ( 20.29) 1166.79 ( 20.18) 1186.97 ( 19.12) 1206.09
8: ( 20.22) 1226.31 ( 20.26) 1246.57 ( 19.12) 1265.70
9: ( 20.15) 1285.85 ( 20.31) 1306.16 ( 19.15) 1325.32
10: ( 20.07) 1345.39 ( 20.36) 1365.74 ( 19.19) 1384.93
11: ( 19.97) 1404.91 ( 20.41) 1425.32 ( 19.25) 1444.57
12: ( 19.88) 1464.44 ( 20.45) 1484.90 ( 19.30) 1504.20
13: ( 19.78) 1523.98 ( 20.48) 1544.46 ( 19.37) 1563.83
14: ( 19.70) 1583.53 ( 20.48) 1604.01 ( 19.47) 1623.47
15: ( 19.59) 1643.06 ( 20.49) 1663.56 ( 19.55) 1683.11
II. y. 1723.11
0: ( 19.51) 1702.61 ( 20.49) 1723.11 ( 19.64) 1742.75
1: ( 19.41) 1762.16 ( 20.49) 1782.66 ( 19.73) 1802.38
2: ( 19.34) 1821.73 ( 20.47) 1842.19 ( 19.84) 1862.03
3: ( 19.26) 1881.29 ( 20.44) 1901.73 ( 19.92) 1921.65
4: ( 19.21) 1940.85 ( 20.41) 1961.26 ( 20.01) 1981.28
5: ( 19.15) 2000.43 ( 20.37) 2020.80 ( 20.08) 2040.88
6: ( 19.14) 2060.02 ( 20.31) 2080.34 ( 20.16) 2100.50
7: ( 19.11) 2119.61 ( 20.25) 2139.86 ( 20.23) 2160.09
8: ( 19.12) 2179.22 ( 20.18) 2199.39 ( 20.30) 2219.70
9: ( 19.12) 2238.82 ( 20.11) 2258.93 ( 20.34) 2279.27
10: ( 19.16) 2298.44 ( 20.01) 2318.45 ( 20.40) 2338.85
11: ( 19.22) 2358.07 ( 19.92) 2377.99 ( 20.44) 2398.43
12: ( 19.27) 2417.70 ( 19.82) 2437.52 ( 20.47) 2457.99
13: ( 19.34) 2477.33 ( 19.73) 2497.06 ( 20.49) 2517.55
14: ( 19.43) 2536.98 ( 19.63) 2556.61 ( 20.49) 2577.10
III. y. 2636.65
0: ( 19.51) 2596.61 ( 19.53) 2616.15 ( 20.51) 2636.65
1: ( 19.60) 2656.26 ( 19.45) 2675.71 ( 20.49) 2696.20
....
| Spörer Gustav, 1822-1895, amateur astronomer, discovered independently from R.Ch.Carrington the time dependence of the occurrence of spots on the distance from the equator - 'Butterfly diagram' and expressed assumption that the Solar activity before y.1716 was very weak. |
Phase of new cycle is always shifted by on an average
(J,S)=19.859 y with regard to the previous cycle.
Phase shifts cause, that the mean cycle of conjunctions (with
regard to intervals of separation) seems to be (statistically,...)
little bit longer, approximately 19.859*(n+1)/n, where n is c.
42-48.
Triads then lasts c. 61 years, i.e. approximately (J,S/2)=60.95
years (1/7 of Babylonian period 427 years).
Long-term changes
Greatest deviations from mean intervals of conjunctions of planet Jupiter and Saturn are caused:
- by planets Jupiter and Saturn itself (elliptical orbits, great inequality)
- by planets Uranus and Neptune (perturbations).
-
Mean cycles of these changes are:
- cycle of 60-61 years (59.58 y, with phase shift, see above)
- cycle of 85.5 years (85.72 y = (U,N)/2 = 171.44/2 y)
Let us try to put these two cycles together.
With regard to phase shifts, we will write one function for
each interval (c. 800-1000 years).
The exact instants of shifts are not clear - perhaps they even
do not exist - one cycle fades while the other one become
stronger:
Interval Function
-----------------------------------------------------------------
(-2000,-1000) |Ap∙sin(2π(t-1111)/P)+Aq∙sin(2π(t-1157)/Q)|
(-1000, 0) |Ap∙sin(2π(t-1131)/P)+Aq∙sin(2π(t-1157)/Q)|
( 0, 1000) |Ap∙sin(2π(t-1151)/P)+Aq∙sin(2π(t-1157)/Q)|
( 1000, 2000) |Ap∙sin(2π(t-1171)/P)+Aq∙sin(2π(t-1157)/Q)|
( 2000, ... ) |Ap∙sin(2π(t-1191)/P)+Aq∙sin(2π(t-1157)/Q)|
....
Here P=3*(J,S)=59.58 y, Q=(U,N)/2=85.72 y, Ap,Aq are
constants and t is time [years]. Values 1111, 1131, 1151, 1171
AD follows c. 20 years phase shifts.
The value 1157 AD was selected 20 years after conjunction (U,N).
Egyptian minimum (-1300,-1200), Homér's minimum (-800,-700)
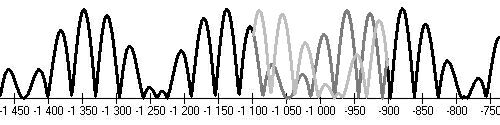
Greek minimum (-450,-350)
|
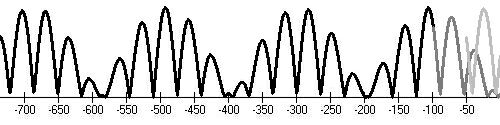
Middle age minimum (650,705)
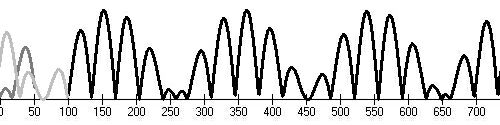
Middle age maximum (1120,1280), Wolf's minimum (1280,1340)
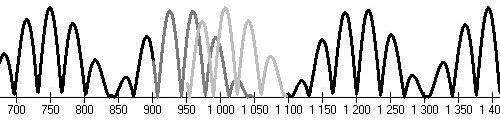
| Maunder, Edward Walter, 1851-1928 English astronomer, dealt with spectroscopy, photography of sunspot, observations of comets, Mars and the like. He confirmed the Spörer's assumption that Solar activity before y.1716 was very weak. |
Sporer's minimum (1400,1500), Maunder's minimum (1645,1715), minimum (1870,1930), end of millenium maximum (1930-2030)
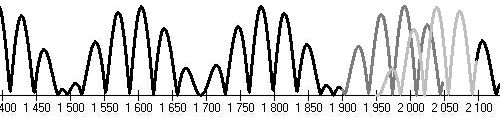
| Eddy, John A., 1931-2009, American astronomer, collected data from a variety of sources and reconstructed retrospectively values of solar activity. He specified period of so called Maunder's minimum (1645-1715) and defined so called Spörer's minimum (1460-1550). |
Comments:
Maunder's minimum started about 1650 AD. An analogous "zero-point" was e.g. at 800 AD, i.e. 850 years (2*B, i.e. 12 Bruckner's cycles) before Maunder's.
- Comparison with Schove's maxima:
- 175-200, (290-300?), 350-375, 500-510, 530, 565, 585, (675?), 745,765,
- (830-840?), 920-930, 960-980, (1100-1150), (1200), 1360-1370,
- 1530-1580, 1720-1740, 1770-1790, (1840-1870?), 1940-1990,...
- Diagrams fail to make clear minimum 1800-1820 AD.
- About 1820 conjunction J-S (1821.76), U-N (1821.01) (and barycentric loop) occured at the same time; J was in perihelion (1821.37).
- G.Sporer called attention to a possible low activity in years 1887-1889.
Other data:
| Minima | Maxima |
|
m2-1: 1040 m2-2: 1160 m2-3: 1270-1330 m2-4: 1410-1500 m2-5: 1670 m2-6: 1820 m2-7: 1880 |
M2-1: 1130 (1100-1150) M2-2: 1190 (1170-1220) M2-3: 1370 M2-4: 1610 M2-5: 1720-1780 M2-6: 1860 M2-7: 1960? |
Synchronization of deviations
Both mentioned cycles coincide with Babylonian period c. 427 years: 61.0 ∙7 = 427.0 years, 85.5 ∙5 = 427.5 years.
Derived periods
[(J,S/2), (U,N)/2]= [60.95, 85.72]= 35.6 years (Bruckner's period),
((J,S/2), (U,N)/2)= (60.95, 85.72)= 210.9 years (half of Babylonian period).
Are these cycles synchronized? Let us assume, it holds:
P=a1*P1+F1 = a2*P2+F2, where a1=14, P1=59.577 years, F1=19.859
years and a2=5, P2= 171.44 y, F2=?
Then P = 14*59.577 + 1*19.859 = 43*19.859 = 853.94 y
(2*B) and phase shift F2 = P- 5*171.44 = -3.27 y.
If F2= 0, then (U,N) = 2*B/5 = 2*36*J/5 = 427.031/5=170.813
y.
And hence Neptunian period: N = ((U,N),U)= (170.813, 84.020)=
165.358 y (deviation 0.4 % from Bretagnon mean period 164.770 y).
Prediction
For years 2000-2700 AD.
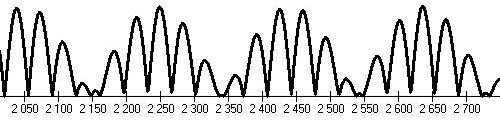
There would be next "Maunder's minima" around years 2150, 2350 and 2500?!.