Schematic algebra - Stratification
Stratification means distribution of instances and classes into levels.
Newton, Isaac| Newton, Isaac |
Partitioning into levels
Binomial theorem
Binomial theorem serves for computation
(a+b)k. Coefficients of particular expressions
as bk−s are caled binomial
coefficients.
![]()
The theorem was formulated by I.Newton, computation of powers
(a+b)k was known already to Italian
mathematicians.
Powers of (a+b)k make system G(2,k) in
the following sense. Nesting is marked by brackeds [].
(a + b)1= a + b
(a + b)²=[a]²+2ab +[b]2
(a + b)³=[a]³+3a²b+3ab²+[b]3
(a + b)4=[a]4+4a³b+4a²b²+2[ab]²+
4ab³+ [b]4
(a + b)5=[a]5+5a4b+10a³b²+10a²b³+5ab4+
[b]5
(a + b)6=[a]6+6a5b+12a4b²+3[a²b]²+18a³b³+2[ab]³+12a²b4+3[ab²]²+
6ab5+[b]6
Because product a∙b needn’t to be commutative, expression a² ∙ b² is not generally equal to [a∙b]² (similarly a4 ∙ b² not corresponds to [a² ∙ b]², ...). In such (non-commutative) case is also ( a + b )² = [a]²+ ab + ba + [b] ²... Leibnitz has derived a similar formula for n-th derivation of product (Leibnitz’s formula).
Binomial coefficients are used also for computation of differential sequences.
Powers (Newton) Derivation (Leibnitz) Difference
(a±b)k (uv)(k) u(k)(n)
───────────────────────────────────────────────────────────
k = 1 a±b u'v+uv' ut+1− ut
k = 2 a²±2ab+b² u''v+2u'v'+uv'' ut+2− 2ut+1 + ut
Stratification in binary system
i gi Binary schema Distance schema Level of class
──────────────────────────────────────────────────────────────
1 0 0000 (0) 0
2 1 0001 0010 0100 1000 (4) 1
3 3 0011 0110 1100 1001 1(3) 2
4 5 0101 1010 2(2) 2
5 7 0111 1110 1101 1011 1 1(2) 3
6 15 1111 1 1 1 (1) 4
Level 0 1 2 3 4
────────────────────────────────────────────
All instances 1 4 6 4 1
Nested instances 1 0 2 0 1
Self instances 0 4 4 4 0
────────────────────────────────────────────
All classes 1 1 2 1 1
Nested classes 1 0 1 0 1
Self classes 0 1 1 1 0
Binomial coefficients determine distribution of all instances into particular levels.
We will be interested also for distribution of self and nested instances, resp. distribution of classes.
Let us compute how many instances a classes in system G(2,4) is on each level.
Nesting in layers
Binomial coefficients of powers (a+b)k arise
from self instances and nested instances of powers
(a+b)d ,d|k, according to schema:
k=1: {1} + {1}
x x
1 1
k=2: 1(1) + {2} + 1(1)
x
1
k=3: 1(1)+ {3} + {3} + 1(1)
x x
1 1
2(2) nested instances
+
k=4: 1(1)+ {4} + {4} + {4} + 1(1) self instances
x x x
1 1 1 self classes
k=5: 1(1)+ {5} + {10} + {10} + {5} + 1(1)
x x x x
1 1 1 1
3(3) 2(2) 3(3)
+ + +
k=6: 1(1)+ {6} + {6} + {6} + {6} + {6} + 1(1)
x x x x x
1 2 3 2 1
k=7: 1(1)+ {7} + {7} + {7} + {7} + {7} + {7} + 1(1)
x x x x x x
1 3 5 5 3 1
2(2)
+
4(4) 4(4) 4(4)
+ + +
k=8: 1(1)+ {8} + {8} + {8} + {8} + {8} + {8} + {8} + 1(1)
x x x x x x x
1 3 7 8 7 3 1
We observe nesting of systems G(2,d) into G(2,k ), d|k, on particular levels. Schema of all instances (Pascal’s triangle) is sum of self instances d(d), where (d) marks number of self classes in system G(2,d).
Extension for n>2
Total number of instances for G(2,k) makes Pascal’s
triangle, generally for G(n,k) arithmetical triangles with base n.
G(2,k) k/L 0 1 2 3 4
──────────────────────────────────────
n=2 0 1
1 1 1
2 1 2 1
3 1 3 3 1
4 1 4 6 4 1
Numbers in Pascal’s triangle are called binomial coefficients. They determine number of ways from the root of the tree into given apex.
k/L 0 1 2 3 ...
──────────────────────────────────────────
n=3 0 1
1 1 1 1
2 1 2 3 2 1
3 1 3 6 7 6 3 1
4 1 4 10 16 19 16 10 4 1
The same holds also generally in arithmetical triangles.
For n=3 each apex of the tree ramify into three directions.
Triangle G(3,k) determine number of possible ways of chess king from edge of chessboard to next fields [Vilenkin].
Similarly self instance split into levels:
k/L 0 1 2 3 4
──────────────────────────────
n=2 0 0
1 1 1
2 0 2 0
3 0 3 3 0
4 0 4 4 4 0
Numbers of nested instances are differences of numbers of all instances and numbers of self instances...
For n=3: (a+b+c)^k
k/L 0 1 2 3 ..
───────────────────────────────────────
n=3 0 0
1 1 1 1
2 0 2 2 2 0 1 1 1
3 0 3 6 6 6 3 0 1 2 2 2 1
4 0 4 8 16 16 16 8 4 0 1 2 4 4 4 2 1
5 0 5 15 30 45 50 45 30 15 5 0 1 3 6 9 10 9 6 3 1
Classes of triads
There are 19 classes of triads in 12-tone musical system -
see the following distance schemas:
11(10) 12(9)
13(8) 14(7) 15(6)
21(9) 22(8)
23(7) 24(6) 25(5)
31(8) 32(7)
33(6) 34(5)
41(7) 42(6)
43(5) 44(4)
51(6)
E.g. schema 21(9), makes 3-sound with whole tone and half tone (e.g. d-e-f), schema 34(5) makes minor triad (e.g. a-c-e), and schema43(5) major triad (e.g. c-e-g).
From these 19 classes, each of 18 classes have 12 transpositions. Only one class with schema 44(4) i.e. augmented triad (e.g. c-e-g#) is nested. This class has 4 instances. Therefore there is (in 12-tone system) 18∙12 = 216 self instances and 1∙4 nested instances, i.e. together 220 instances of triads and these triads makes 18 (self) + 1 (nested) = 19 classes.
Stratification instances and classes
Total number of nested instances as well as nested classes in system with prime k is equal to 2.
Number of self instances is always k-multiple of number of self classes:
V=k∙v
Method of nesting triads is depicted in the column (3) of the following table:
k (0)(1)(2)(3) (4) (5) (6) (7) (8) (9)(10)(11)(12) ───────────────────────────────────────────────────────────────── 12 1 12 66 220 495 792 924 792 495 220 66 12 1 všechny instance (M) ───────────────────────────────────────────────────────────────── 1 1 1 2 0 2 0 3 0 3 3 0 vnořené instance (W) 4 0 4 4 4 0 6 0 6 12 18 12 6 0 ──────────────────────────────────────────────────────────────── 12 0 12 60 216 480 792 900 792 480 216 60 12 0 vlastní instance (V) - − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − 12 0 1 5 18 40 66 75 66 40 18 5 1 0 vlastní druhy (v) ───────────────────────────────────────────────────────────────── 1 1 1 2 0 1 0 3 0 1 1 0 vnořené druhy (w) 4 0 1 1 1 0 6 0 1 2 3 2 1 0 ───────────────────────────────────────────────────────────────── 12 1 1 6 19 43 66 80 66 43 19 6 1 1 všechny druhy (m)
We get number of all instances (M) by return from numbers of self instances (V):
M(12,0) = V(12,0) + V(12,1) = 0 + 1 = 1
M(12,1) = V(12,1) = 12
M(12,2) = V(12,2) + V(6,1) = 60 + 6 = 66
M(12,3) = V(12,3) + V(4,1) =216 + 4 = 220
Triangles
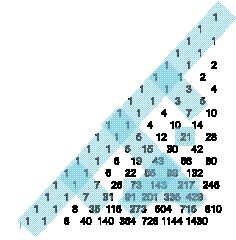
Triangles of numbers, that we will observe, arise from numbers of instances and classes in particular systems G(2,k). Triangles are symmetric, so it is enough to write half of them.
First column displays order k of given G-system, second column total number of elements (instances, classes). In the next columns are numbers of elements for particular levels L=0..κ(k).
Triangle of binomial coefficients (Pascal’s triangle) was known several thousand years ago, it was found in old Chinese records.
Pascal, Blaise| Pascal, Blaise [paskal], 1623-1662, |
Instance triangles
Triangle of all instances (Pascal triangle)k [M(2,k)] M(2,k,L) 0 [ 1] 1 1 [ 2] 1 2 [ 4] 1 2 3 [ 8] 1 3 4 [ 16] 1 4 6 5 [ 32] 1 5 10 6 [ 64] 1 6 15 20 7 [ 128] 1 7 21 35 8 [ 256] 1 8 28 56 70 9 [ 512] 1 9 36 84 126 10 [ 1024] 1 10 45 120 210 252 11 [ 2048] 1 11 55 165 330 462 12 [ 4096] 1 12 66 220 495 792 924 13 [ 8192] 1 13 78 286 715 1287 1716 14 [ 16384] 1 14 91 364 1001 2002 3003 3432 15 [ 32768] 1 15 105 455 1365 3003 5005 6435 16 [ 65536] 1 16 120 560 1820 4368 8008 11440 12870 17 [131072] 1 17 136 680 2380 6188 12376 19448 24310 18 [262144] 1 18 153 816 3060 8568 18564 31824 43758 48620 19 [524288] 1 19 171 969 3876 11628 27132 50388 75582 92378
k [W(2,k)] W(2,k,L) 0 [ 1] 1 1 [ 0] 0 2 [ 2] 1 0 3 [ 2] 1 0 4 [ 4] 1 0 2 5 [ 2] 1 0 0 6 [ 10] 1 0 3 2 7 [ 2] 1 0 0 0 8 [ 16] 1 0 4 0 6 9 [ 8] 1 0 0 3 0 10 [ 44] 1 0 5 0 0 32 11 [ 2] 1 0 0 0 0 0 12 [ 76] 1 0 6 4 15 0 24 13 [ 2] 1 0 0 0 0 0 0
k [V(2,k)] V(2,k,L) 0 [ 1] 0 1 [ 2] 1 2 [ 2] 0 2 3 [ 6] 0 3 4 [ 12] 0 4 4 5 [ 30] 0 5 10 6 [ 54] 0 6 12 18 7 [ 126] 0 7 21 35 8 [ 240] 0 8 24 56 64 9 [ 504] 0 9 36 81 126 10 [ 990] 0 10 40 120 200 250 11 [ 2046] 0 11 55 165 330 462 12 [ 4020] 0 12 60 216 480 792 900 13 [ 8190] 0 13 78 286 715 1287 1716
Class triangles
Triangle of all classesk [m(2,k)] m(2,k,L) 0 [ 1] 1 1 [ 2] 1 2 [ 3] 1 1 3 [ 4] 1 1 4 [ 6] 1 1 2 5 [ 8] 1 1 2 6 [ 14] 1 1 3 4 7 [ 20] 1 1 3 5 8 [ 36] 1 1 4 7 10 9 [ 60] 1 1 4 10 14 10 [ 108] 1 1 5 12 21 28 11 [ 188] 1 1 5 15 30 42 12 [ 352] 1 1 6 19 43 66 80 13 [ 632] 1 1 6 22 55 99 132
k [w(2,k)] w(2,k,L) 0 [ 1] 1 1 [ 0] 0 2 [ 2] 1 0 3 [ 2] 1 0 4 [ 3] 1 0 1 5 [ 2] 1 0 0 6 [ 5] 1 0 1 1 7 [ 2] 1 0 0 0 8 [ 6] 1 0 1 0 2 9 [ 4] 1 0 0 1 0 10 [ 9] 1 0 1 0 2 1 11 [ 2] 1 0 0 0 0 0 12 [ 17] 1 0 1 1 3 0 5 13 [ 2] 1 0 0 0 0 0 0
k [v(2,k)] v(2,k,L) 0 [ 0] 0 1 [ 2] 1 2 [ 1] 0 1 3 [ 2] 0 1 4 [ 3] 0 1 1 5 [ 6] 0 1 2 6 [ 9] 0 1 2 3 7 [ 18] 0 1 3 5 8 [ 30] 0 1 3 7 8 9 [ 56] 0 1 4 9 14 10 [ 99] 0 1 4 12 20 25 11 [ 186] 0 1 5 15 30 42 12 [ 335] 0 1 5 18 40 66 75 13 [ 630] 0 1 6 22 55 99 132
Triangle of self classes is analysed in separate chapter.
Substitution
Triangles can be mathematically contracted to half size – by
substitution. Let us set (a+b)k a=x and b=1/x and
yj = xj+ 1/xj, so y1 = x+1/x, y2 =
x²+1/x²... Coefficients of new expressions
cover just half of coefficients from Pascal’s triangle:
y1 = y1
y1² = (x+1/x)² =
x²+2+1/x² = y2+ 2
y1³ = (x+1/x)³ =
x³+3(x+1/x)+1/x³ = y3+ 3y1
y14 = (x+1/x)³ = .... = y4+ 4y2+
6
Goniometrical functions
Let us compute expression (c−s)5 according to
binomial theorem: The fifth row of Pascal’s triangle
is
1 5 10
10 5 1
And therefore
(c−s)5 = c5 −5c4s
+10c³s²−10c²s³+5cs4
−s5
Now let us mark s=sin(x), c= cos(x), t = tan(x). It
holds:
cos(5x) = c5 −10c³s²
+5cs4
sin(5x) = 5c4s
−10c²s³ +s5
tan(5x) = (t5 +10t³
+5t)/(1−10t²+5t4)
Congruence of triangles
If we substitute numbers in triangle T by their remainders according to certain module r, we get new triangle T(r).
Let us observe properties of these triangles.
Triangle of all instances
Pascal’s triangle according to module 2 has fractal structure
and corresponds to so called Sierpinski’s triangle. Binary numbers
in particular rows makes products of odd Fermat’s numbers
{3,5,15,17,51,85,255,257,...} (see Gauss' polygons).
T(2) k L B Partition Indexes
─────────────────────────────────────────────────────────────
1 0 1 1 1 −
1 1 1 2 3 3 0
1 0 1 2 2 5 5 1
1 1 1 1 3 4 15 3∙5 0,1
1 0 0 0 1 4 2 17 17 2
1 1 0 0 1 1 5 4 51 3∙17 0,2
1 0 1 0 1 0 1 6 4 85 5∙17 1,2
1 1 1 1 1 1 1 1 7 8 255 3∙5∙17 0,1,2
1 0 0 0 0 0 0 0 1 8 2 257 257 3
1 1 0 0 0 0 0 0 1 1 9 4 771 3∙257 0,3
1 0 1 0 0 0 0 0 1 0 1 10 4 1285 3∙257 1,3
1 1 1 1 0 0 0 0 1 1 1 1 11 8 3855 3∙5∙257 0,1,3
1 0 0 0 1 0 0 0 1 0 0 0 1 12 4 4369 17∙257 2,3
1 1 0 0 1 1 0 0 1 1 0 0 1 1 13 8 13107 3∙17∙257 0,2,3
Level binary numbers (i.e. number of digits 1) in
particular rows is given by expression L = 2m, where m
is number of primes in partition.
For k=2t numbers gets form 2(2t)+1 (see
F-systems).
T(2) k L Polynomial
───────────────────────────────────────────────────────────
1 0 1 1
1 1 1 2 x+1
1 0 1 2 2 x²+1
1 1 1 1 3 4 x³+x²+x+1
1 0 0 0 1 4 2 x4+1
1 1 0 0 1 1 5 4 x5+x4+x+1 =(x4+1)∙(x+1)
1 0 1 0 1 0 1 6 4 x6+x4+x²+1 =(x4+1)∙(x²+1)
1 1 1 1 1 1 1 1 7 8 x7+x6+x5+x4+x³+x²+x+1
1 0 0 0 0 0 0 0 1 8 2 x8+1
1 1 0 0 0 0 0 0 1 1 9 4 x9 +x8+x+1 =(x8+1)∙(x+1)
Derived triangles
Triangle of self classes arise by division of triangle of self instances. Odd number has always odd divisors only and for prime k triangles of self and of all elements (instances, classes) (excluding marginal instances) coincide. Therefore for odd prime k distribution of even and odd numbers in mentioned triangles is the same as in Pascal’s triangle.
Triangle of self instances has for odd k the same structure as triangle of self classes. Numbers B in rows of triangle of self instances are for even k all zero.
Triangle of self classes
T(2) k L B Partition Correction
────────────────────────────────────────────────────────
0 0 0 0 0
1 1 1 2 3 3
1 2 1 1 1
1 1 3 2 3 3
1 1 1 4 3 7 7
1 0 0 1 5 2 9 3²
1 0 1 0 1 6 3 21 3∙7 3∙7
1 1 1 1 1 1 7 6 63 3²∙7 3∙3∙7
1 1 1 0 1 1 1 8 6 119 7∙17
1 0 1 0 0 1 0 1 9 4 165 3∙5∙11 3∙5∙11
1 0 0 0 1 0 0 0 1 10 3 273 3∙7∙13 3∙7∙13
1 1 1 0 0 0 0 1 1 1 11 6 903 3∙7∙43 21∙43
1 1 0 0 0 1 0 0 0 1 1 12 5 1571 1571
1 0 0 1 1 0 0 1 1 0 0 1 13 6 2457 3³∙7∙13 7∙13∙27
There are pairs of numbers a,b that keep relation b=2a±1 in the last column. They exist for all prime k<=13, does it hold also for some higher values of k?
Triangle of all classes
T(2) k L B Partition
─────────────────────────────────────────────────────
1 0 1 1 1
1 1 1 2 3 3
1 1 1 2 3 7 7
1 1 1 1 3 4 15 3∙5
1 1 0 1 1 4 4 27 3³
1 1 0 0 1 1 5 4 51 3∙17
1 1 1 0 1 1 1 6 6 119 7∙17
1 1 1 1 1 1 1 1 7 8 255 3∙5∙17
1 1 0 1 0 1 0 1 1 8 6 427 7∙61
1 1 0 0 0 0 0 0 1 1 9 4 771 3∙257
1 1 1 0 1 0 1 0 1 1 1 10 8 1879 1879
1 1 1 1 0 0 0 0 1 1 1 1 11 8 3855 3∙5∙257
1 1 0 1 1 0 0 0 1 1 0 1 1 12 8 6939 3∙2313
1 1 0 0 1 1 0 0 1 1 0 0 1 1 13 8 13107 3∙17∙257
Rows in triangle of nested instances and also in triangle of nested classes are for prime k of form xk+1.
In triangle of nested instances have the same form also for k=2t (as well as in Pascal’s triangle).
Zeroising of triangles
Clearing sequences
Let us mark numbers in k−th row of triangle c(k,s) and let us look for such sequence of numbers d(s), i.e.{d0,d1,d2,...}, to keep:
∑c(k,s)∙d(s) = 0 (for s=0,..,k)
d0+d1= 1-1= 0 d0+2d1+d2= 1-2+1= 0 d0+3d1+3d2+d3= 1-3+3-1= 0
Let us constrain to sequence with d0=1. To nullify Pascal’s triangle
sequence {1,−1,1,−1,...} is needed:
d0+d1=1-1= 0 d0+2d1+d2=1-2+1= 0 d0+2d1+2d2+d3=1-2+2-1= 0 d0+3d1+4d2+3d3+d4=1-3+4-3+1= 0
This sequence is nullified also by triangle
of all classes without marginal members:
d0+d1= 1 -1= 0 d0+d1+d2= 1-1+0= 0 d0+2d1+2d2+d3= 1-2+0+1= 0 d0+2d1+3d2+2d3+d4= 1-2+0+2-1= 0
Triangle of self classes is nullified by sequence
{1,−1,0,1,−1,0,...}:
Stirling’s triangle of 1.druhu is nullified by unitary sequence {1,1,1,1,...}, Stirling’s triangle of 2.druhu by alternating sequence of factorials {1,−1,2,−6,24,−120,...}, see Stirling’s triangles.
Bernoulli’s numbers
Now let us make the same without the last member in each row of triangle of self classes. We will sum:
∑c(k,s)∙d(s) = 0 (for s=0,..,k−1)
(We could also skip the first member -instead of the last- and consider expression:
(b+1)k−bk
i.e. so called Kronecker’s δ (delta)).In Pascal’s triangle we get system of equations:
d0+2d1 = 0
d0+3d1+3d2 = 0
d0+4d1+6d2+4d3 = 0
d0+5d1+10d2+10d3+5d4 = 0
Thereof (after substitution d0=1) we get sequence {1,−1/2,1/6,0,−1/30,0,1/42,0,−1/30,...}. Members of this sequence are so called Bernoulli’s numbers. All Bernouli’s numbers with odd indexes except B1=−1/2 are zero.
Numbers was introduced by Jacob Bernoulli in the formula for
sum of integer powers. They are used for summing of progressions
(e.g. sum of Lerch’s progressions ∑nk∙f(n,k), where
f(n,k) are Fermat’s coefficients), in theory of differential
sequences, in Kummer’s theory of regular primes, in mathematical
analysis,...
In progression x/(1−e−x) Bernouli’s numbers are
the coefficients at xn/n!:
d0+d1 = 0 d0+2d1+2d2 = 0 d0+2d1+3d2+2d3 = 0 d0+3d1+5d2+5d3+3d4 = 0 d0+3d1+7d2+8d3+7d4+3d5 = 0
Analogy of Bernoulli‘s numbers
From triangle of self classes we get equation:
Z nich (for d0=1) we get sequence
{1,−1,1/2,−1/4,+1/4,−5/12,..}.
d0+2d1 = 0 d0+2d1+2d2 = 0 d0+3d1+4d2+3d3 = 0 d0+3d1+5d2+5d3+3d4 = 0
Thereof sequence {1,−1/2,1/6,−1/9,...}.
Möbius‘s function
Möbius, August Ferdinand| Möbius, August Ferdinand [], 1790-1868 |
So called Möbius' function μ(k) was defined by A.F.Möbius (1832), but before him the same function was used by C.F.Gauss (1801) . Gauss has proved that sum of primitive roots for given module depends on this function and similar computation used also later.
Parity of prime factors
Definition of Möbius' function is simple, but it is is a bit peculiar and difficult to understand.
Value μ(k) depends on number of prime factors of number k, it determine their parity..
-
In case of even numbers μ(k)=+1, in opposite case μ(k)=−1.
E.g. μ(15)=μ(3∙5) = +1, μ(30)=μ(2∙3∙5) = −1.
- For number 1 is defined μ(1)=1. All primes p have odd parity, i.e. μ(p)=−1.
- If n is divisible by some square (i.e. by second power, excluding number 1) then μ(n)=0.
μ(k)=−1: 2,3,5,7,11,13,17,19,23,29,30,31,37,41,42,43,47,...
μ(k)= 0: 4,8,9,12,16,18,20,24,25,27,28,32,36,40,44,45,48,49,50,...
μ(k)=+1: 1,6,10,14,15,21,22,26,33,34,35,38,39,46,...
Sum of primitive roots
Sum of primitive roots according to module r is determined by Möbius' function μ(r−1):
r Primitive roots Sum mod r Partition of r−1 μ(r−1) ──────────────────────────────────────────────────────────────── 11 2,6,7, 8 23 1 10 = 2∙5 1 13 2,6,7,11 26 0 12 = 3∙2² 0 31 3,11,12,13,17,21,22,24 123 −1 30 = 2∙3∙5 −1
Sums through divisors
The following sums go through all divisors d of number k, i.e. d|k (k>1).
Sum Möbius' functions of divisors is zero:
∑(μ(d)) = 0
For number of divisors τ(d) it holds:
∑(μ(d)∙τ(k/d))=∑(μ(k/d)∙τ(d)) = 1
For sum of divisors σ(d) it holds:
∑(μ(d)∙σ(k/d))=∑(μ(k/d)∙σ(d)) = k
Euler’s function is determined by relation:
φ(k)=∑(μ(d)∙k/d)=∑(μ(k/d)∙d)
E.g. for k=12 (φ(12) = 4):
d μ(d) k/d μ(d)∙k/d Děl.k/d τ(k/d) μ(d)∙τ(k/d) σ(k/d) μ(d)∙σ(k/d) ────────────────────────────────────────────────────────────────────────────── 1 1 12 12 1,2,3,4,6,12 6 6 28 28 2 −1 6 −6 1,2,3,6 4 −4 12 −12 3 −1 4 −4 1,2,4 3 −3 7 −7 4 0 3 0 1,3 2 0 4 0 6 1 2 2 1,2 2 2 3 3 12 0 1 0 1 1 0 1 0 ───────────────────────────────────────────────────────────────────────────── x ∑0 x 4 x 1 x 12
| Landau, Edmund [], 1877-1938 |
Mangoldt‘s relation
E.Landau has proved:
∑(μ(n)/n) = 0
for n=1..∞
I.e.: 1−1/2−1/3−1/5+1/6−1/7+1/10−1/11−1/13+1/14+1/15−1/17−1/19+... = 0
Binomial self instances
Let us consider case k=6 of binomial equation xk−1=0 (see). System M6(x) contains systems M2(x) and M3(x), and these contains M1(x).
Let us write in short composition of systems. We will compare composition of expression to values of Möbius' function for particular numbers d|k.
d k/d μ(d) ────────────────────────────── 1 6 1 M1 = V1 2 3 −1 M2 = V1∙V2 3 2 −1 M3 = V1∙V3 6 1 1 M6 = V1∙V2∙V3∙V6
Let us compute V6; expressions Mk/d for that μ(d)=1 are in numerator, expressions with μ(d)=−1 are in denominator: V6 = M6/(V1∙V2∙V3) = M6∙M1/(M2∙M3)
Generally it holds:
Vk(x) = ∏[Mk/d(x)]μ(d)
Aplication in G-systems
Number of self classes
To determine number self classes Gauss uvádí the following rule [Gauss II]:
|
Now it is easy to derive from this theorem meaning of expression (n);... If n= aa bb cc..., where a,b,c,... are distinct primes, then n(n)=pn − ∑pn/a+ ∑pn/ab−∑pn/abc+..., where ∑pn/abc.. denote set of all expressions of type pn/abc.., where quantities a,b,c,... anyhow rearrange. So e.g. for n=36: 36(36)=p36−p18−p12+p6 |
Let us clear this example. Number 36 has partition into product of primes 36 = 2²∙3². So particular members of expression for 36∙v(p,36) have exponents:
36 = 36, 36/2 = 18, 36/3 = 12 a 36/2/3 = 6
Let us determine number of self classes v(n,36) according to Gauss' rule from relation:
v(n,36) = (n36−n18−n12+n6)/36
Let us note, that the sign is determined by values of Möbius' function for particular divisors of numbers 36.
Stratification of instances and classes
Numbers in table of stratification of instances and classes can be derived with help of Möbius' function [Read].
From nk instances we get value V(2,12) by count out of nested instances, i.e. these, that have d transpositions, where d|k (d≤k):
V(n,k) = ∑(μ(k/d)∙nd), for d|k
For n=2, k=12:
d k/d nd μ(k/d) μ(k/d)∙nd M(n,k)−V(n,d)
────────────────────────────────────────────────────────
12 1 4096 1 4096 4096
6 2 64 −1 −64 −(6+12+18+12+6)=−54
4 3 16 −1 −16 −(4+4+4)=−12
3 4 8 0 0 −(3+3)=−6
2 6 4 +1 +4 −2
1 12 2 0 0 −(1+1)=−2
────────────────────────────────────────────────────────
4020 4020
It holds V(2,12) = 4020 = 12∙335=12∙v(12,2), i.e. relation gives correct number of self instances V(n,k).
But counts out (e.g.−64,−16) resp. counts in (+4) of instances does not express numbers of nested instances from particular G(n,d).
Gauss‘s theorem
Because number of self instances must be always divisible by order k, it holds:
V(n,k) ≡ 0 (mod k)
Therefore for n,kεN it holds [Narkiewicz] (sum for d|k):
∑(μ(k/d) nd) ≡ 0 (mod k)
The relation was proved by Gauss (1846) for kεP, demonstration for kεN was completed later by J.A.Serret.
E.g. for n=2
for k=3: 21μ(3)+ 2³μ(1) = 2∙(−1)+8 = 6 ≡ 0 (mod 3)
for k=9: 21μ(9)+ 2³μ(3)+ 29 μ(1)= 2∙0 +8∙(−1)+ 512= 504 ≡ 0 (mod 9)
for k=6: 21μ(6)+ 2²μ(3)+ 2³ μ(2) + 26 μ(1)= 2∙1 +4∙(−1)+ 8∙(−1) + 64 = 54 ≡ 0 (mod 6)
Sternek’s relation
Let F(n) = ∏f(n/d)μ(d). Then each prime, that divide F(n), divide also f(n), but not divide f(i) for i=1,2,...,n−1 (R.D.von Sternek,1896).
Dedekind, Richard| Dedekind, Richard [], 1831-1916, |
Law of inversion of numeric functions
The following two relations are equivalent: (Dedekind (1857), Liouville (1857)),[Vinogradov]
∑ f(d) = g(k), for d|k, k≥1
∑ μ(d) g(k/d) = f(k) for d|k, k≥1
Modifiction of binomial theorem
Differences of the form u'(t) = ut+1− ut can in some cases appear to be unnatural. We will try to show, that it is more suitable to use the form
u'(t) = ut+1−a∙ut
where a is some number.
Powers of algebraic numbers
Let us consider powers of algebraic numbers (a+b√d)t = vt+ ut√d. We begin with cases a=b=1 for d=2 and d=3:
(1+√2)1 = 1 + 1√2 (1+√3)1 = 1 + 1√3 (1+√2)2 = 3 + 2√2 (1+√3)2 = 4 + 2√3 (1+√2)3 = 7 + 5√2 (1+√3)3 = 10 + 6√3 (1+√2)4 = 17 + 12√2 (1+√3)4 = 28 + 16√3 (1+√2)5 = 41 + 29√2 (1+√3)5 = 76 + 44√3 (1+√2)6 = 99 + 70√2 (1+√3)6 =208 + 120√3
Numbers vt makes here the first differential sequence of numbers ut:
Coefficients (1+√2)k Coefficients (1+√3)k
─────────────────────────────────────────────────────────
1 2 5 12 29 70 169 s(0,t)=ut 1 2 6 16 44 120 328..
1 3 7 17 41 99 . s(1,t)=vt 1 4 10 28 76 208 .
2 4 10 24 58 .. s(2,t) 3 6 18 48 132 ..
2 6 14 34 ... s(3,t) 3 12 30 84 ..
4 8 20 ... s(4,t) 9 18 54 ..
4 12 ... s(5,t) 9 36 ...
8 .. s(6,t) 27 ...
Pisot‘s numbers
Real numbers that powered to high exponent approach natural numbers are called Pisot’s numbers.
E.g. number [(√ 5+1)/2]99 has dot followed by 20 zeros, number [(√ 5+1)/2]100 has dot followed by 20 digits 9.
Let us notice sequence of ratios in the previous
schemas:
{1/1,3/2,7/5,17/12,41/29,99/70,239/169,... }. Values of
fractions approach value √2.
Therefore 5∙√2=7.07107, 29∙√2 = 41.01219, 169∙√2 = 239.00209.
It is why powers of Pisot’s algebraic numbers go near to
natural numbers.
Differential sequences
Let us mark h-th differential sequence s(h,t). Every second row is 2-times multiple of original row for d=2, e.g. {2,6,14,34,..} = 2∙ {1,3,7,17,..}, 3-times multiple for d=3, e.g. {3,12,30,84,..} = 3∙ {1,4,10,28,..} and so on. In case a=b=1 it holds:
s(h+2,t) = d ∙ s(h,t)
For negative d are sequences less regural, but relation of differential sequences keeps:
Coefficients (1+√−2)k
──────────────────────────────────────────────────
+1 +2 +1 −4 −11 −10 +13 +56 ... s(0,t)=ut
+1 −1 −5 −7 +1 +23 +43 ... s(1,t)=vt
−2 −4 −2 +8 +22 +20 ... s(2,t)
−2 +2 +10 +14 −2 ... s(3,t)
4 8 4 −16 ... s(4,t)
4 −4 −20 ... s(5,t)
−8 −16 ... s(6,t)
Recurrent relations
Let use rewrite relation s(h+2,t) = d ∙ s(h,t) to form of differential equation u''(t) − u(t)∙d = 0.
If we define:
u'(t) = ut+1−ut
u''(t) = ut+2−2ut+1+ ut
we get:
u''(t) − u(t)∙d = 0
ut+2−2ut+1+ ut− ut∙d = 0
ut+2 = 2ut+1+(d−1)ut
resp.
ut = 2ut−1+(d−1)∙ut−2
In case a=b=1 it is not necessary to compute powers of
algebraic numbers. Coefficients ut follows from
given recurrent relations, coefficients vt are their
first differential sequences.
E.g. for d=2, ut = 2ut−1+
ut−2, i.e. ut = {1, 2, 2∙2+1=5, 2∙5+2=12,
2∙12+5 = 29, ...}
General case of powers
In general case of powers (a+b√d)t the previous relations fail. We have to change computation of differential sequences.
E.g. in cases a=2 b=1 for d=2 a d=3 we get:
(2+√2)1 = 2 + 1√2 (2+√3)1 = 2 + 1√3 (2+√2)2 = 6 + 4√2 (2+√3)2 = 7 + 4√3 (2+√2)3 = 20 + 14√2 (2+√3)3 = 26 + 15√3 (2+√2)4 = 68 + 48√2 (2+√3)4 = 97 + 56√3 (2+√2)5 =232 +164√2 (2+√3)5 =362 +209√3
Sequence vt does not make differential sequence of ut and we can’t get relations analogical to relations in the previous paragraphs.
Let us correct definition of differential sequences:
u'(t) = ut+1−a∙ut
u''(t)= (ut+2−a∙ut+1)− (ut+1−a∙ut)= ut+2−(a+1)ut+1+ a∙ut
We get:
Coefficients (2+√2)k Coefficients (2+√3)k
───────────────────────────────────────────────────────────
1 4 14 48 164 ... s(0,t)=ut 1 4 15 56 209 ...
2 6 20 68 ... s(1,t)=vt 2 7 26 97 ...
2 8 28 ... s(2,t) 3 12 45 ...
4 12 ... s(3,t) 6 21 ...
4 ... s(4,t) 9 ...
Now sequence vt are differential sequences of ut and relation (derived in the previous paragraphs) holds:
s(h+2,t) = d ∙ s(h,t)
Symbolic notation
Powers (a+b√d)t:
(a+b√d)1= a + b√d (a+b√d)2= a2+ b2d + b(2a)√d (a+b√d)3= a3+ 3ab2d + b(3a2+b2d)√d (a+b√d)4= a4+ 6a2b2d+ b4d2 + b(4a3+4ab2d)√d (a+b√d)5= a5+10a3b2d+ 5ab4d2 + b(5a4+10a2b2d+b4d2)√d (a+b√d)6= a6+15a4b2d+15a2b4d2+b6d3 + b(6a5+20a3b2d+6ab4d)√d
Differential sequences:
1 2a 3a²+b²d 4a³+4ab²d 5a4+10a²b²d+b4d² a5+6ab4d²+20a³b²d
a a²+b²d a³+3ab²d a4+6a²b²d+b4d² a5+10a³b²d+5ab4d²
b²d 2ab²d 3a²b²d+b4d² 4a³b²d+4ab4d²
ab²d a²b²d+b4d² a³b²d+ 3ab4d²
b4d² 2ab4d²
ab4d²
In case, when differential sequences respect relation u'(t) = ut+1−a∙ut are coefficients of powers of algebraic numbers determined by recurrent sequences according to relation:
s(h+2,t) = b²d ∙ s(h,t)
Golden number
Number (√5−1)/2 is called golden number (in connection to Fibonacci’s sequence and golden section) . Similarly silver number ((√8−2)/2 and bronze number (√13−3)/2 were derived. For such numbers xk it holds xk = 1/(k+xk), so xk is (positive) solution of equation x²+kx−1 =0.
E.g. for k=2 gets equation x²+2x−1=0 solution (−2+√8)/2 [= √2−1], i.e. silver number.
Euler‘s number
From sequences of factorials and super-factorials (see Factorials) come these algebraic numbers:
2 + 1√d 326 + 120√d 5 + 2√d 1957 + 720√d 16 + 6√d .... 65 + 24√d
Values of fractions { 2/1,5/2,16/6,65/24,326/120,1957/720,... } get near to the Euler’s number e.
Is it possible to set operation (to select value d,..) in
a such way, that algebraic numbers satisfy (power) relation?