The Last Fermat's Theorem - Power sequences

You're reading an English translation of the original Czech page.

Characteristics of power seuences 

Characteristics of power sequences 
for k=0..5: 
    • k=0: [1] 
    • k=1: [1,0] 
    • k=2: [2,1,0] 
    • k=3: [6,6,1,0] 
    • k=4: [24,36,14,1,0] 
    • k=5: [120,240,150,30,1,0]

In power sequences {f(t)} =tk is c(k)=k! and for k>0 is c(1)=1 and c(0)=0. For c(2) is (0+1)∙2=2, (2+1)∙2=6, (6+1)∙2=14, (14+1)∙2=30, i.e. coefficients c(2) make sequence defined by recurrent rule f(k+1)=(f(k)+1)∙2.

Generally it holds:

r(m) = f_sum_t_0-m f_binom04 ∙(t−m)k = f_sum_t_0-m (−1)k∙ f_binom04 ∙(m−t)k

When m>k is c(m)=0. f_binom05

E.g. for k=4, m=0..4:

r(0)= f_binom_0_0 ∙04=0

r(1)= f_binom_1_0 ∙14− f_binom_1_1 ∙04=1−0=1

r(2)= f_binom_2_0 ∙24− f_binom_2_1 ∙14+ f_binom_2_2 ∙04=16−2+0=14

r(3)= f_binom_3_0 ∙34− f_binom_3_1 ∙24+ f_binom_3_2 ∙14− f_binom_3_3 ∙04=81−48+3−0=36

r(4)= f_binom_4_0 ∙44− f_binom_4_1 ∙34+ f_binom_4_2 ∙24− f_binom_4_3 ∙14+ f_binom_4_4 ∙04=256−324+96−4+0=24
─────────────────────────────────────────────
For m=5 is:
r(5)= f_binom_5_0 ∙54− f_binom_5_1 ∙44+ f_binom_5_2 ∙34− f_binom_5_3 ∙24+ f_binom_5_4 ∙14− f_binom_5_5 ∙04
=625−1280+810−160+5−0= 0

Because if m=k is r(k)=k!, then r(k)=∑ f_binom27 ∙(t−k)k = k!

Power sequences

Let us check on simple example of sequences of 2.order, that in power sequences [2,1,0] corresponds indexes (a,b,c) to F-sum a²+b²=c².
By transformation from [0,0,0] to [2,1,r0] we get:
r0 = 2∙( 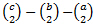f_binom_cba2) + 1∙( f_binom_cba1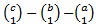) = 2∙t(c−1)/2−2∙s(b−1)/2−2∙r(a−1)/2 + 1∙(c−b−a) = c²−b²−a²
In case r0=0 is therefore a²+b²=c².

Similarly in sequences of 3.order transformation from [0,0,0,0] to [6,6,1,r0] provides:
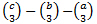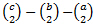r0 =6∙( f_binom_cba3) + 6∙( f_binom_cba2) + 1∙( f_binom_cba1 ).
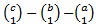For c is 6∙t(c−1)(c−2)/6 + 6∙t(c−1)/2 + 1∙(c) = c³−3l²+2l + 3l²−3l+c = c³.
Proto when r0=0, is a³+b³=c³.

Shifts of power sequences

Shift of order 0: F-sum f(a)+f(b)=f(c) with F-indexes (a,b,c) exists in power sequences shifted by v,

i.e. {f(n)} = {nk+v}, if v = ck−bk−ak.
E.g. for k=2 and indexes (1,2,3) we get v=3²−2²−1² = 9−4−1=4.

Therefore F-sum with indexes (1,2,3) appears in sequences with characteristic [2,1,4]: 

Charakter. Sequence                    F-indexes  F-sum
──────────────────────────────────────────────────────────
[2,1,0]    {0,1,4,9,16,25,36,49,... }  (3,4,5)    9+16=25
[2,1,1]    {1,2,5,10,17,26,37,50,...}  (4,8,9)    17+65=82
[2,1,2]    {2,3,6,11,18,27,38,51,...}  (3,5,6)    11+27=38
[2,1,3]    {3,4,7,12,19,28,39,52,...}  (0,1,2)    3+4=7
[2,1,4]    {4,5,8,13,20,29,40,53,...}  (1,2,3)    5+8=13
[2,1,5]    {5,6,9,14,21,30,41,54,...}  (0,2,3)    5+9=14

Shift of order 1: F-sum f(a)+f(b)=f(c) with F-indexes (a,b,c) exists in sequences shifted by v∙n, i.e. {f(n)} = {nk+v∙n}, if:

v = (ck−bk−ak)/(c−b−a)

For k=3 and indexes (2,3,4) we get v= 4³−3³−2³ = 64−27−8 = 29.

Therefore F-sum with indexes (2,3,4) appears in sequences with characteristic [6,6,30,0]: 

n          0   1   2   3    4    5    6
────────────────────────────────────────
[6,6,1,0]  0   1   8  27   64  125  216 
29∙n       0  29  58  87  116  145  174 
────────────────────────────────────────
[6,6,30,0] 0  30  66 114 180   270  390    66+114 = 180

Generalization:
Let us consider change of sequence after shift of their m-th differential sequence by value v.

Then in the new sequence are all the original members shifted by v∙ f_binom50 , i.e. {f(n)}={nk+v∙ f_binom50 }.

In this new sequence there exists F-sum f(a)+f(b)=f(c) with indexes (a,b,c) if:

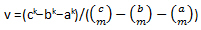
f_binom_expr_v

Sequences of characteristics

Characteristics [6,6,1,r]

The sequence of third powers has a characteristic [6,6,1,0]. Let's look at what must be sequences with the characteristic [h, h, 1, r] to have the F-sum with indices (a, b, c).

For the value r we get the expression:

r = (h/6)*(c3-b3) + ((6-h)/6)*(t-s) - a3

For h = 6, the second summer is dropped and the expression is reduced to r = c3-b3- a3.          Indeed, there are a number of sequences that have indices (a, b, c) and characteristics [6,6,1, r].          But there is no one with r = 0, ie with [6,6,1,0]. 

Charakter.  F-indexy      F-součet     Posloupnost
──────────────────────────────────────────────────────────
[6,6,1,7]   (0,1,2)         7+8=15     {7,8,15,34,71,132,223,350,519,...}
[6,6,1,26]  (0,1,3)       26+27=53     {26,27,34,53,90,151,242,369,538,...}
[6,6,1,63]  (0,1,4)       63+64=127    {63,64,71,90,127,188,279,406,575,...}
[6,6,1,124] (0,1,5)     124+125=249    {124,125,132,151,188,249,340,467,636,...}
[6,6,1,215] (0,1,6)     215+216=431    {215,216,223,242,279,340,431,558,727,...}
[6,6,1,342] (0,1,7)     342+343=685    {342,343,350,369,406,467,558,685,854,...}
[6,6,1,511] (0,1,8)     511+512=1023   {511,512,519,538,575,636,727,854,1023,...}
[6,6,1,728] (0,1,9)     728+729=1457   {728,729,736,755,792,853,944,1071,1240,...}
[6,6,1,19]  (0,2,3)       19+27=46     {19,20,27,46,83,144,235,362,531,748,1019,...}
[6,6,1,56]  (0,2,4)       56+64=120    {56,57,64,83,120,181,272,399,568,785,1056,...}
[6,6,1,117] (0,2,5)     117+125=242    {117,118,125,144,181,242,333,460,629,846,...}
[6,6,1,208] (0,2,6)     208+216=424    {208,209,216,235,272,333,424,551,720,937,...}
[6,6,1,335] (0,2,7)     335+343=678    {335,336,343,362,399,460,551,678,847,1064,...}
[6,6,1,504] (0,2,8)     504+512=1016   {504,505,512,531,568,629,720,847,1016,1233,...}
[6,6,1,721] (0,2,9)     721+729=1450   {721,722,729,748,785,846,937,1064,1233,1450,...}
[6,6,1,37]  (0,3,4)       37+64=101    {37,38,45,64,101,162,253,380,549,766,1037,...}
[6,6,1,98]  (0,3,5)      98+125=223    {98,99,106,125,162,223,314,441,610,827,1098,...}
[6,6,1,189] (0,3,6)     189+216=405    {189,190,197,216,253,314,405,532,701,918,...}
[6,6,1,316] (0,3,7)     316+343=659    {316,317,324,343,380,441,532,659,828,1045,...}
[6,6,1,485] (0,3,8)     485+512=997    {485,486,493,512,549,610,701,828,997,1214,...}
[6,6,1,702] (0,3,9)     702+729=1431   {702,703,710,729,766,827,918,1045,1214,1431,...}
[6,6,1,61]  (0,4,5)      61+125=186    {61,62,69,88,125,186,277,404,573,790,1061,...}
[6,6,1,152] (0,4,6)     152+216=368    {152,153,160,179,216,277,368,495,664,881,...}
[6,6,1,279] (0,4,7)     279+343=622    {279,280,287,306,343,404,495,622,791,1008,...}
[6,6,1,448] (0,4,8)     448+512=960    {448,449,456,475,512,573,664,791,960,1177,...}
[6,6,1,665] (0,4,9)     665+729=1394   {665,666,673,692,729,790,881,1008,1177,...}
[6,6,1,91]  (0,5,6)      91+216=307    {91,92,99,118,155,216,307,434,603,820,...}
[6,6,1,218] (0,5,7)     218+343=561    {218,219,226,245,282,343,434,561,730,947,...}
[6,6,1,387] (0,5,8)     387+512=899    {387,388,395,414,451,512,603,730,899,1116,...}
[6,6,1,604] (0,5,9)     604+729=1333   {604,605,612,631,668,729,820,947,1116,1333,...}
[6,6,1,127] (0,6,7)     127+343=470    {127,128,135,154,191,252,343,470,639,856,...}
[6,6,1,296] (0,6,8)     296+512=808    {296,297,304,323,360,421,512,639,808,1025,...}
[6,6,1,513] (0,6,9)     513+729=1242   {513,514,521,540,577,638,729,856,1025,1242,...}
...

The expression for r does not have to be quite obvious at the first look at the sequence.              E.g. by gradual generalization of partial sequences for [6,6,1, r] we get the form:         

r = n3-3*b*n2) + 3*b2*n - a3

where n = (t-s). After substitution we will then get r = c3-b3- a3.

Catalan's formulas

We will follow some special cases of relations described above in the part F-sums in seuences in the following paragraphs.

We are looking for all sequences f= {f(i)} having such members f(a),f(b),f(c), that so called F-sum f(a)+f(b)=f(c) holds.

We are interested in how these relations ( in case of sequence f(n) = nk ) influence on the posibility of solution ak +bk =ck (Last Fermat theorem says, that such solution do not exists).

Let us focus on the case k=3 first. We observe arithmetic sequences of the 3-th order ( 3-th differential sequence is constant ).

Such sequence is e.g. {0,18,42,78,132,210,... } 

 0,  18,   42,   78,   132,  210, ...   given sequence {f(t)}
    18,  24,   36,    54,  78, ...      1. differential {d1(t)}
        6,    12,   18,   24,   ...     2. differential {d2(t)}
           6,    6,    6,  ...          3. differential {d3(t)}

This sequence has characteristic

[6,6,18,0] (number on the left) - r0=0,r1=18,r2=6,r3=6.

In this sequence it holds 78+132=210, so, we say, there exists F-sum:

(3,4,5) ~ f(3) +f(4) = f(5) .

On the contrary we know that in sequence {0,1, 8,27,64,125,216,... } with characteristic [6,6,1,0] no such F-sum exists.

The prove (for k=3) was already done - firstly by L. Euler (1707-1783) and J.L. Lagrange (1736-1813).

What is the distinction of the two sequences ( [6,6,18,0] and [6,6,1,0])?

When there exists some F-sum and when not?

Sequences [6,6,r,0]

In the following outline there are sequences with characteristics [6,6,r,0], where r=1,2,..30, their firs existing F-sum (in first 100 members of each sequence) and coresponding F-indexes. 

Charakter.   Sequence                      F-indexes    F-sum
──────────────────────────────────────────────────────────────────────────
[6,6,1,0]     {0,1,8,27,64,125,216,... }
[6,6,2,0]     {0,2,10,30,68,130,222,...}  ( 36, 37, 46) 46692+50690=97382
[6,6,3,0]     {0,3,12,33,72,135,228,...}  ( 10, 12, 14) 1020+1752=2772
[6,6,4,0]     {0,4,14,36,76,140,234,...}  ( 10, 18, 19) 1030+5886=6916
[6,6,5,0]     {0,5,16,39,80,145,240,...}  ( 72, 74, 92) 373536+405520=779056
[6,6,6,0]     {0,6,18,42,84,150,246,...}  (  8, 13, 14) 552+2262=2814
[6,6,7,0]     {0,7,20,45,88,155,252,...}  ( 13, 27, 28) 2275+19845=22120
[6,6,8,0]     {0,8,22,48,92,160,258,...}  ( 29, 63, 65) 24592+250488=275080
[6,6,9,0]     {0,9,24,51,96,165,264,...}  ( 20, 24, 28) 8160+14016=22176
[6,6,10,0]    {0,10,26,54,100,170,...  }  (  4,  5,  6) 100+170=270
[6,6,11,0]    {0,11,28,57,104,175,...  }
[6,6,12,0]    {0,12,30,60,108,180,...  }  (  5,  7,  8) 180+420=600
[6,6,13,0]    {0,13,32,63,112,185,...  }  ( 20, 36, 38)  8240+47088=55328
[6,6,14,0]    {0,14,34,66,116,190,...  }  ( 39, 80, 83) 59826+513040=572866
[6,6,15,0]    {0,15,36,69,120,195,...  }  ( 15, 34, 35) 3585+39780=43365
[6,6,16,0]    {0,16,38,72,124,200,...  }  (  8,  9, 11) 632+864=1496
[6,6,17,0]    {0,17,40,75,128,205,...  }
[6,6,18,0]    {0,18,42,78,132,210,...  }  (  3,  4,  5) 78+132=210
[6,6,19,0]    {0,19,44,81,136,215,...  }  ( 30, 36, 42) 27540+47304=74844
[6,6,20,0]    {0,20,46,84,140,220,...  }  ( 12, 13, 16) 1956+2444=4400
[6,6,21,0]    {0,21,48,87,144,225,...  }  ( 13, 28, 29) 2457+22512=24969
[6,6,22,0]    {0,22,50,90,148,230,...  }  (  4,  6,  7) 148+342=490
[6,6,23,0]    {0,23,52,93,152,235,...  }
[6,6,24,0]    {0,24,54,96,156,240,...  }  (  5,  8,  9) 240+696=936
[6,6,25,0]    {0,25,56,99,160,245,...  }  ( 26, 54, 56) 18200+158760=176960
[6,6,26,0]    {0,26,58,102,164,250,... }
[6,6,27,0]    {0,27,60,105,168,255,... }  ( 13, 15, 18) 2535+3765=6300
[6,6,28,0]    {0,28,62,108,172,260,... }  ( 30, 54, 57) 27810+158922=186732
[6,6,29,0]    {0,29,64,111,176,265,... }
[6,6,30,0]    {0,30,66,114,180,270,... }  (  2,  3,  4) 66+114=180

We will derive relation for r as function a,b,d: r=F(a,b,d) from observation F-sums (a, b, b+d) for d=1,2,... :

For d=1: 

    Charakter.     Sequence         F-indexes     F-sum

    ────────────────────────────────────────────────────-─────────────────────

    [6,6,30,0]     {0,30,66,114,180,270,... } (  2,  3,  4) 66+114=180
    [6,6,54,0]     {0,54,114,186,276,390,...} (  2,  4,  5) 114+276=390
    [6,6,84,0]     {0,84,174,276,396,540,...} (  2,  5,  6) 174+540=714
    ...
    [6,6,18,0]     {0,18,42,78,132,210,... }  (  3,  4,  5) 78+132=210
    [6,6,33,0]     {0,33,72,123,192,285,... } (  3,  5,  6) 123+285=408
    ...

r = 3 * b(b+1)/(a-1) - a(a+1), for example when a=2, b=3 then r = 3*3*4/1 - 2*3 = 30, for a=3, b=5 is r = 3*5*6/2 - 3*4 = 33.

For d=2:
    Charakter.     Sequence      F-indexes     F-sum
    ────────────────────────────────────────────────────-─────────────────────
    [6,6,37,0]     {0,37,80,135,208,305,... } (  8, 10, 12) 800+1360=2160
    [6,6,60,0]     {0,60,126,204,300,420,...} (  8, 11, 13) 984+1980=2964
            ...

r = 6 * b(b+2)/(a-2) - a(a+2) - 3, for example when a=8, b=11 then r = 6*11*13/6 - 8*10 - 3 = 60


Let us mark c=b+d. In sequence with characteristic [6,6,r,0] there exists F-sum (a, b, c) = (a, b, b+d), when it holds:

r = 3*d*b*(b+d)/(a-d) - a(a+d) - d² + 1

Not existing F-sums

In sequences with characteristic [6,6,r,0] there exists F-sums (5,7,8), (5,8,9),(5,11,12), (5,12,13), it is (5, b, b+1) just for some b.

For example for b=9 such sums do not exists. It follows from the derived relation for a=5,b=9, d=1:

r = 3*d*b*(b+d)/(a-d) - a(a+d) - d² + 1 = 3*1*9*10/4 - 5*6 - 1 + 1 = 75/2 = 37.5

Not-existence of any F-sum is caused by fact, that expresion 3*d*b*(b+d) is not multiple of (a-d),

so it do not hold: (a-d) | 3*d*b*(b+d).


Power sequence

In sequence with characteristic [6,6,1,0] is r=1. When it holds a³+b³=(a+d)³, then 1 = 3*d*b*(b+d)/(a-d) - a(a+d) - d² + 1, so

3*d*b*(b+d)/(a-d) - a(a+d) - d² = 0

By multiplication (a-d) we get:

3*d*b*(b+d) = a³- d³

3*d*b*c = a³- d³

From relation 3dbc=a³-d³ it follows, that d | a³ and therefore if the number a is prime (aεP), then there is d=1.

In general case ap +bp = cp (pεP) it holds: p < a < b < c < (a+b).

If b*c divide the expression a³-d³= (a-d) * (a²+ad+d2 ), then there is necessarily ( b*c, a-d) > 1 or b*c | a²+ad+d2.

Catalan, Charles Eugene
Catalan, Charles Eugene [], 1814-1894, belgian matematician working in France and Belgium. In addition to number theory he was engaged also by descriptive geometry and combinatorics.

Catalan's formula for d=1

In case d=1 (a εN) i.e. 3b(b+1)= a³-1 have to be 3 | a³-1, what exclude 3 | a .

Because a³-1 = (a-1) (a²+a+1), there must be 3 | a-1 or 3 | a²+a+1; but the condition for the second is a=1 (mod 3),

so again 3 | a-1.

Charles E. Catalan has derived (y.1886) in general case ap +bp =(b+1)p (p εP), the following formula: